'남한산성'(김훈)을 읽고
0. 최근 영화 '남한산성'이 개봉하면서 'JTBC 뉴스룸'에 '김훈'작가가 출현한 적이 있다. 이 때 인터뷰가 인상에 남아 책을 꼭 읽어보고자 하였다. 인터뷰 내내 묻어나는 그의 말에 대한 집념은 매력적이었다. 애초에 소설에 별 관심이 없는 나지만, 이 책은 꼭 한번 읽어보고 싶었다.
1. 소설의 말은 건조하고 담담하다. 어느 한 구석 감성에 젖어 격한 말을 내뿜는 곳이 없다. 그럼에도 머릿속에 그려지는 시린 서울의 풍경과, 남한산성 안에서의 고단함은 소설 내내 나를 짓눌렀다. 이미 역사로 알고있는 '병자호란'과 '삼전도 굴욕'의 사이 내용을 그의 상상력과 필체로 저술했다.
이판 최명길은 청과 화친하여 이 위기를 넘고자 했고, 예판 김상헌은 끝까지 싸우길 원했다. 그들은 쇠락해가던 명나라와 오랑캐(여진)에서 세력이 커져 중국 대륙을 쓸어담기 시작한 청나라 사이에서 갈등했다. 어찌보면 반도에 위치한 소국에게는 피할 수 없는 운명이었으리라. 이 사이에서 현실감각 없는 관료들은 공허한 말만 내뱉는다. 대표적으로 영의정 김류가 그랬다. 그리고 그 사이에 낀 왕은 무기력했다. 묘당 아래서 각자의 위치를 지닌 사람들은 스스로 그 위치를 지켰다. 수어사 이시백이 그랬고, 대장장이 서날쇠가 그랬다.
2. 이 소설의 좋은 점은 단순히 정치가의 시각만 가지고 쓴 것이 아니라는 점이다.
소위 천민들은 명이고, 청이고 상관없이 전쟁이 끝나기를 바랐다.
김상헌에게 목이 베인 사공은 그저 본인이 살기위한 길을 찾아가는 것 뿐이었다. 그에게 그 것이 반역이라고 생각할 겨를은 없었을 것이다. 노비였던 정명수는 청으로 투항하여 통역일을 하며 전횡을 일삼았다.
대장장이 서날쇠가 그나마 본인의 삶에 애착을 갖는 인물이다. 그는 김상헌을 도와 격서를 돌리기도 하고, 사공의 딸 나루를 거두어 키운다. 전쟁이 끝나고 본인의 자리로 돌아와 다시 그 삶을 지속한다.
소설 내내 그들의 고단함이 몸으로 느껴진다.
3. 개인적으로 강요된 애국과 충성을 싫어한다. 결국 본인들의 터전에 대한 애착이 있어야 애국이란 것도 생기고, 외부의 적을 맞아 싸울 힘이 생긴다고 생각한다. 그래서 소설 속에 그려진 일반 백성들의 모습이 나에겐 그리 낯설지 않았다. 그만큼 그당시 정치가 일반 백성들과는 멀리 떨어져있었고, 어떤 공감대도 나누지 못했다는 증거인 것 같다. 청에 끌려갔다 돌아와 독살당한(것으로 추정되는) 소현세자가 더욱 애처롭게 느껴진다.
8. .ARIMA + GARCH를 이용한 시계열 예측
ARIMA(p, d, q) 모형은 시계열을 d번 차분하여 고정된 시계열(stationary time series)를 얻을 수 있다. 하지만 시계열을 구성하는 분산을 고정해야하는 단점이 있다. 이렇게 분산을 고정할 경우 주기 시계열처럼 변동성 군집(volatility clustering) 현상이 있는 시계열 분석이 어렵다는 단점이 있다.
이러한 단점을 해결하는 방법이 GARCH(r, s)와 같은 이분산 모형을 이용하여 시계열의 분산 자체를 모형화 하는 방법이다. 하지만 이 경우 시계열의 전체적인 방향성을 이해하는데는 문제가 있다.
최근 알고리즘 트레이딩 분야에서 나름 주목을 받는 방법이 앞의 두 모형을 섞어 사용하는 것이다. 전체적인 방향성은 ARIMA 모형으로 찾고, 시계열의 분산을 GARCH로 분석하여 예측하는 방식이다.
다음의 ARIMA(p, d, q)를 보자.
$$
\theta_p(\mathbf{B})(1-\mathbf{B})^d x_t = \phi_q(\mathbf{B})\epsilon_t
$$
여기서 $d=0$일 경우 ARMA(p, q)와 동일하므로 다음의 식으로 나타낼 수 있다.
$$
x_t = \sum^{p}_{i=1} \alpha_i x_{t-i} + \sum^{q}_{j=1} \beta_j \epsilon_{t-j} + \epsilon_t
$$
ARMA는$\epsilon_t$로 표현하는 충격 또는 오류항이 동일한 분산을 갖는다고 정의한다. 이 부분에 GARCH(r, s)를 적용하여 $\epsilon_t$를 다음과 같이 정의한다.
$$
\epsilon_t = \sigma_t \omega_t \\
\sigma^2_t = \alpha_0 + \sum_{i=1}^r \alpha_i \epsilon_{t-i}^2 + \sum_{j=1}^s \beta_j \epsilon_{t-j}^2
$$
이렇게 정의한 후 시계열에 적용하면, 시계열의 방향성을 찾으면서 이분산 특정도 잡아낼 수 있다.
이 책에서 예제로 제시한 것은 S&P500 지수에 대한 예측과 이에 따른 전략이었다. 하지만 구글 파이낸스가 지수 정보는 제공하지 않는 관계로 구글의 주가를 가지고 전략을 테스트 해보았다. ARIMA+GARCH를 이용하여 다음날의 주가 방향을 예측하고 상승이면 long, 하락이면 short 포지션을 취한다.
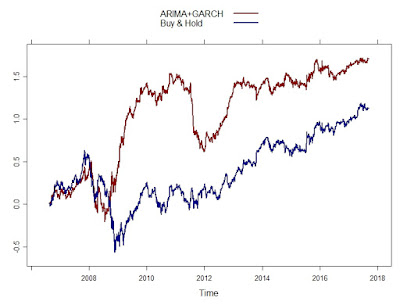
그 결과는 다음의 그래프이다.
그래프의 붉은 선이 전략에 의한 수익이고, 푸른색 선이 주식을 사고 버텼을 경우의 수익이다. 2008년에서 2010년 사이 금융위기 당시 하락 추세에서 short 포지션을 잘 취하여 높은 수익을 낸다. 하지만 2012년 경 시장이 혼조세를 겪으면서 예측이 틀리고 큰 손실이 발생하는 것을 볼 수 있다. 이 부분에서 어떻게 예측력이 떨어진것인지 연구해 볼 가치가 있다고 생각한다.
ARIMA+GARCH를 이용하여 시계열을 맞추는 코드는 다음과 같으며, R을 이용한 코드이다.
이러한 단점을 해결하는 방법이 GARCH(r, s)와 같은 이분산 모형을 이용하여 시계열의 분산 자체를 모형화 하는 방법이다. 하지만 이 경우 시계열의 전체적인 방향성을 이해하는데는 문제가 있다.
최근 알고리즘 트레이딩 분야에서 나름 주목을 받는 방법이 앞의 두 모형을 섞어 사용하는 것이다. 전체적인 방향성은 ARIMA 모형으로 찾고, 시계열의 분산을 GARCH로 분석하여 예측하는 방식이다.
다음의 ARIMA(p, d, q)를 보자.
$$
\theta_p(\mathbf{B})(1-\mathbf{B})^d x_t = \phi_q(\mathbf{B})\epsilon_t
$$
여기서 $d=0$일 경우 ARMA(p, q)와 동일하므로 다음의 식으로 나타낼 수 있다.
$$
x_t = \sum^{p}_{i=1} \alpha_i x_{t-i} + \sum^{q}_{j=1} \beta_j \epsilon_{t-j} + \epsilon_t
$$
ARMA는$\epsilon_t$로 표현하는 충격 또는 오류항이 동일한 분산을 갖는다고 정의한다. 이 부분에 GARCH(r, s)를 적용하여 $\epsilon_t$를 다음과 같이 정의한다.
$$
\epsilon_t = \sigma_t \omega_t \\
\sigma^2_t = \alpha_0 + \sum_{i=1}^r \alpha_i \epsilon_{t-i}^2 + \sum_{j=1}^s \beta_j \epsilon_{t-j}^2
$$
이렇게 정의한 후 시계열에 적용하면, 시계열의 방향성을 찾으면서 이분산 특정도 잡아낼 수 있다.
이 책에서 예제로 제시한 것은 S&P500 지수에 대한 예측과 이에 따른 전략이었다. 하지만 구글 파이낸스가 지수 정보는 제공하지 않는 관계로 구글의 주가를 가지고 전략을 테스트 해보았다. ARIMA+GARCH를 이용하여 다음날의 주가 방향을 예측하고 상승이면 long, 하락이면 short 포지션을 취한다.
그 결과는 다음의 그래프이다.
그래프의 붉은 선이 전략에 의한 수익이고, 푸른색 선이 주식을 사고 버텼을 경우의 수익이다. 2008년에서 2010년 사이 금융위기 당시 하락 추세에서 short 포지션을 잘 취하여 높은 수익을 낸다. 하지만 2012년 경 시장이 혼조세를 겪으면서 예측이 틀리고 큰 손실이 발생하는 것을 볼 수 있다. 이 부분에서 어떻게 예측력이 떨어진것인지 연구해 볼 가치가 있다고 생각한다.
ARIMA+GARCH를 이용하여 시계열을 맞추는 코드는 다음과 같으며, R을 이용한 코드이다.
library(quantmod)
library(lattice)
library(timeSeries)
library(rugarch)
# S&P 500 주가를 받고 NA는 없앰
getSymbols("GOOG", from="1990-01-01", src = "google")
gg_returns = diff(log(Cl(GOOG)))
gg_returns[as.character(head(index(Cl(GOOG)), 1))] = 0
# foreacst vector를 만들어 예측치 저장
window_len = 500
fore_len = length(gg_returns) - window_len
forecasts <- vector(mode="character", length=fore_len)
for(d in 0:fore_len)
{
# rolling window를 구함
gg_returns_offset = gg_returns[(1+d):(window_len + d)]
# fitting ARIMA model
final.aic <- Inf
final.order <- c(0, 0, 0)
for(p in 0:5)
{
for(q in 0:5)
{
if(p == 0 && q==0)
{
next
}
arima_fit = tryCatch(arima(gg_returns_offset, order = c(p, 0, q)),
error = function(err) FALSE,
warning = function(err) FALSE)
if(!is.logical(arima_fit))
{
current.aic <- AIC(arima_fit)
if(current.aic < final.aic)
{
final.aic <- current.aic
final.order <- c(p, 0, q)
final.arima <- arima(gg_returns_offset, order = final.order)
}
}
else
{
next
}
}
}
# fitting GARCH model
spec = ugarchspec(
variance.model = list(garchOrder=c(1,1)),
mean.model = list(armaOrder=c(final.order[1], final.order[3]), include.mean=T),
distribution.model="sged"
)
fit = tryCatch(
ugarchfit(
spec, gg_returns_offset, solver = 'hybrid'
), error=function(e) e, warning=function(w) w
)
# GARCH 모형이 수렴하지 않으면 방향을 "long"으로 선택
# 그렇지 않으면 수익률 예측에 따라 맞는 방향을 찾아줌
if(is(fit, "warning"))
{
forecasts[d + 1] = paste(
index(gg_returns_offset[window_len]), 1, sep=","
)
print(
paste(
index(gg_returns_offset[window_len]), 1, sep=","
)
)
}
else
{
fore = ugarchforecast(fit, n.ahead = 1)
ind = fore@forecast$seriesFor
forecasts[d + 1] = paste(
colnames(ind), ifelse(ind[1] < 0, -1, 1), sep=","
)
print(
paste(
colnames(ind), ifelse(ind[1] < 0, -1, 1), sep=","
)
)
}
}
# forecast 결과를 csv에 씀
write.csv(forecasts, file="E:/devel/R_src/AdvAlgoTrading/forecasts.csv", row.names=FALSE)
7. ARIMA, ARCH 모형
이 포스트는 AR과 MA를 혼합한 ARMA에서 한 발 더 나아간 ARIMA 모형을 소개한다. 그리고 시점마다 분산이 변하는 시계열을 처리하기 위한 이분산(heteroskedastic) 모형을 소개한다.
ARMA 모형의 경우 불안정(non-stationary) 시계열을 모델링하는데 적합하지 않다. 하지만 불안정 시계열의 차분을 새로운 시계열로 만들면 안정적(stationary) 시계열이 될 수 있다. 이 점이 ARIMA 모형을 사용하게하는 중요한 이유이다.
ARIMA 모형은 ARIMA(p, d, q)로 표현한다. 여기서 p와 q는 앞선 포스트에서 소개한 AR과 MA의 차수이고, d는 몇 번의 차분을 수행하는가의 의미이다. (차분이 왜 integrated라는 이름을 달고있는가는 이해하지 못했다.)
ARIMA(p, d, q)는 d번의 차분을 시계열에 수행했을 때, 그 시계열이 ARMA(p, q) 모형을 따른다는 의미이다. 이를 식으로 정의하면 다음과 같다.
$$
\theta_p(\mathbf{B})(1-\mathbf{B})^d x_t = \phi_q(\mathbf{B})\omega_t
$$
이식을 ARMA(p, q)를 나타내는 $\theta_p(\mathbf{B})x_t = \phi_q(\mathbf{B})\omega_t$와 비교하면 그 차이를 명확히 알 수 있다.
다음의 코드는 Amazon의 시계열을 받아와 ARIMA모형으로 피팅하는 R 코드이다.
이 코드에서 AIC 함수를 이용하여 ARIMA(p, d, q)의 각 차수를 결정하는 것을 볼 수 있다.
앞서 ARMA 계열의 모형은 어찌했건 시계열의 안정적 상태를 가정한다. 즉, 분산이 시점에 상관없이 같은 값을 갖는다고 가정한다. 하지만 이와 다르게 분산이 시점에 따라 달라지는 시계열을 자주 볼 수 있으며, 이를 시계열이 이분산(heteroskedastic) 특성을 갖는다고 한다. 이와 더불어 이분산 특성이 연속적으로 연관되어 나타난다면, 특정 조건하에서 이분산이 나타나는 것이므로 이를 조건부 이분산(conditional heteroskedastic) 특성이라 한다.
이런 특성을 갖는 시계열을 분석하기 위해 변동성 자체를 모형으로 만드는 ARCH나 GARCH 모형을 사용할 수 있다. 차수가 1인 ARCH(1) 모형은 시계열 $\{ \epsilon_t \}$에 대해 다음과 같이 정의한다.
$$
\epsilon_t = \sigma_t \omega_t \\
\sigma_t^2 = \alpha_0 + \alpha_1 \epsilon_{t-1}^2
$$
위의 식을 $\epsilon_t$에 대해 풀면 다음과 같다.
$$
\epsilon_t = \omega_t \sqrt{\alpha_0 + \alpha_1 \epsilon_{t-1}^2}
$$
위의 식을 p 차수로 확장한 ARCH(p)의 식은 다음과 같다.
$$
\epsilon_t = \omega_t \sqrt{\alpha_0 + \sum_{i=1}^p \alpha_i \epsilon_{t-i}^2}
$$
여기서 $\alpha$는 모형 인수이다.
GARCH(Generalized Autoregressive Conditional Heteroskedastic) 모형은 ARCH(p)를 확장한 모형으로서, GARCH(p, q)로 표현한다. 표현식은 다음과 같다.
$$
\epsilon_t = \sigma_t \omega_t \\
\sigma^2_t = \alpha_0 + \sum_{i=1}^p \alpha_i \epsilon_{t-i}^2 + \sum_{j=1}^q \beta_j \epsilon_{t-j}^2
$$
여기서 $\alpha$와 $\beta$는 모형의 인수이다. GARCH는 ARCH에 이동 평균(moving average) 항을 추가한 모형으로 이해할 수 있다.
1. ARIMA(Autoregressive Integrated Moving average)
ARMA 모형의 경우 불안정(non-stationary) 시계열을 모델링하는데 적합하지 않다. 하지만 불안정 시계열의 차분을 새로운 시계열로 만들면 안정적(stationary) 시계열이 될 수 있다. 이 점이 ARIMA 모형을 사용하게하는 중요한 이유이다.
ARIMA 모형은 ARIMA(p, d, q)로 표현한다. 여기서 p와 q는 앞선 포스트에서 소개한 AR과 MA의 차수이고, d는 몇 번의 차분을 수행하는가의 의미이다. (차분이 왜 integrated라는 이름을 달고있는가는 이해하지 못했다.)
ARIMA(p, d, q)는 d번의 차분을 시계열에 수행했을 때, 그 시계열이 ARMA(p, q) 모형을 따른다는 의미이다. 이를 식으로 정의하면 다음과 같다.
$$
\theta_p(\mathbf{B})(1-\mathbf{B})^d x_t = \phi_q(\mathbf{B})\omega_t
$$
이식을 ARMA(p, q)를 나타내는 $\theta_p(\mathbf{B})x_t = \phi_q(\mathbf{B})\omega_t$와 비교하면 그 차이를 명확히 알 수 있다.
다음의 코드는 Amazon의 시계열을 받아와 ARIMA모형으로 피팅하는 R 코드이다.
require(quantmod)
getSymbols("AMZN", src="google")
# close price
amzn = diff(log(Cl(AMZN)))
plot(amzn)
# remove na
ft <- as.numeric(amzn)
ft <- ft[!is.na(ft)]
# fitting ARIMA
ftfinal.aic <- Inf
ftfinal.order <- c(0, 0, 0)
for(p in 1:4)
{
for(d in 0:1)
{
for(q in 1:4)
{
ftcurrent.aic <- AIC(arima(ft, order=c(p, d, q)))
if(ftcurrent.aic < ftfinal.aic)
{
ftfinal.aic <- ftcurrent.aic
ftfinal.order <- c(p, d, q)
ftfinal.arima <- arima(ft, order=ftfinal.order)
}
}
}
}
ftfinal.order
이 코드에서 AIC 함수를 이용하여 ARIMA(p, d, q)의 각 차수를 결정하는 것을 볼 수 있다.
2. ARCH(Autoregressive Conditional Heteroskedastic)과 GARCH 모형
앞서 ARMA 계열의 모형은 어찌했건 시계열의 안정적 상태를 가정한다. 즉, 분산이 시점에 상관없이 같은 값을 갖는다고 가정한다. 하지만 이와 다르게 분산이 시점에 따라 달라지는 시계열을 자주 볼 수 있으며, 이를 시계열이 이분산(heteroskedastic) 특성을 갖는다고 한다. 이와 더불어 이분산 특성이 연속적으로 연관되어 나타난다면, 특정 조건하에서 이분산이 나타나는 것이므로 이를 조건부 이분산(conditional heteroskedastic) 특성이라 한다.
이런 특성을 갖는 시계열을 분석하기 위해 변동성 자체를 모형으로 만드는 ARCH나 GARCH 모형을 사용할 수 있다. 차수가 1인 ARCH(1) 모형은 시계열 $\{ \epsilon_t \}$에 대해 다음과 같이 정의한다.
$$
\epsilon_t = \sigma_t \omega_t \\
\sigma_t^2 = \alpha_0 + \alpha_1 \epsilon_{t-1}^2
$$
위의 식을 $\epsilon_t$에 대해 풀면 다음과 같다.
$$
\epsilon_t = \omega_t \sqrt{\alpha_0 + \alpha_1 \epsilon_{t-1}^2}
$$
위의 식을 p 차수로 확장한 ARCH(p)의 식은 다음과 같다.
$$
\epsilon_t = \omega_t \sqrt{\alpha_0 + \sum_{i=1}^p \alpha_i \epsilon_{t-i}^2}
$$
여기서 $\alpha$는 모형 인수이다.
GARCH(Generalized Autoregressive Conditional Heteroskedastic) 모형은 ARCH(p)를 확장한 모형으로서, GARCH(p, q)로 표현한다. 표현식은 다음과 같다.
$$
\epsilon_t = \sigma_t \omega_t \\
\sigma^2_t = \alpha_0 + \sum_{i=1}^p \alpha_i \epsilon_{t-i}^2 + \sum_{j=1}^q \beta_j \epsilon_{t-j}^2
$$
여기서 $\alpha$와 $\beta$는 모형의 인수이다. GARCH는 ARCH에 이동 평균(moving average) 항을 추가한 모형으로 이해할 수 있다.
도구로써의 Machine Learning
최근 기술의 발달은 꿈의 기술이라 불리는 인공지능(AI)를 가까이서 체험할 수 있는 계기를 만들어 주었다. '무어의 법칙'으로 대변할 수 있는 컴퓨터의 발달은 이미 개인용 기기가 수십년 전 메인프레임급의 컴퓨팅 파워를 갖게했다. 그리고 그것을 넘어 직접 서버를 사지 않고도 클라우드 컴퓨팅을 통해 초고성능 컴퓨터를 어디에서나 사용할 수 있게됐다.
뉴럴네트워크를 위시한 인공지능 알고리즘은 1943년 처음 모형이 등장했고, 1980년대 연결주의란 이름으로 뇌의 뉴런 연결을 모형화하기 이른다. 하지만 지금에 비하면 조악한 컴퓨팅 파워로 인해 큰 발전을 하지못했고, 2000년대 중반까지도 발전이 더딘 분야였다. 하지만 컴퓨터 자체의 연산 능력이 늘어남은 물론, 클라우드 컴퓨팅 모델이 발달하면서 큰 전기가 마련된다. 특히 클라우드 컴퓨팅은 저렴한 비용으로 고성능 서버의 묶음을 사용하게 한다. 그럼으로써 비용만 충분히 지불한다면 거의 원하는만큼의 컴퓨터를 이용하여 뉴런의 연결을 표현할 수 있다. 그로인해 더 다양한 알고리즘이 등장한다. 특히 2010년경 발표된 'Recursive Neural Network'은 자연어, 시계열 등의 처리에 있어 획기적인 전기를 마련한다. 게다가 구글에서 발표한 'Tensorflow'와 이를 쉽게 사용하기 위한 API까지 등장해 사용자 접근성 또한 획기적으로 높아졌다.
이런 큰 발전에 힘입어 일반 사용자들도 그 혜택을 보기 시작했다. 개인이 집에 둘 수 있는 인공지능 스피커가 있다. 이 스피커는 사용자의 말을 받아들여 연결되어있는 서버에서 답변을 처리해 사용자에게 돌려준다. 아x존의 에x, SxT의 누x 등이 있다. 스마트폰은 이미 S사와 A사가 모두 인공지능 비서를 내부에 탑재하고 있다. 그 외에 바둑을 스포츠로 삼는 동아시아권에서 구x 알파고의 승전보는 매우 큰 충격을 안겨주었다. 이렇다 보니 각종 매체에서 인공지능으로 대체될 직업의 이야기가 심심치않게 보이고, 마치 터x네이터2에서 보던 종말이 다가온 것이 아닌가 하는 영화적 걱정도 보인다.
내 의견은 그런 걱정이 너무 지나치다는 것이다. 인공지능의 사용 추세를 보면 이미 변혁을 일으키기 위한 임계치 근처에 와 있다는 판단은 든다. 이미 사람들이 알게 모르게 인공지능을 접하고 있고, 많은 산업이 인공지능을 도입하여 생산성을 높이려 하고있다. 아마 조금의 시간이 지나면 스마트폰이나 인터넷이 그랬듯이 인공지능도 당당하게 필수 도구의 한 자리를 차지할 것이다. 그렇다면 인터넷과 스마트폰에 빗대어 앞으로를 예상해볼 수 있을 것 같다.
스마트폰이나 인터넷이 등장하고 기술이 발전하면서 사라지거나 힘이 약해진 직업들이 있다. 전화 교환원, 타자를 대신 쳐주던 타자원, 인쇄에 꼭 필요하던 식자공 등이 있다. 하지만 그에 반해 생긴 직업도 있다. 각 회사마다 상주하는 네트워크 관리를 하는 사람, 스마트폰을 파는 사람, 스마트폰 어플리케이션을 개발하는 사람 등 다양하다. 즉, 기술의 발전이 단순히 파괴적 상황만을 가져왔다고 보기 힘들다는 이야기다.
아직 어떤 방향으로 흐를지 정확히 예측하긴 어려우나, 인공지능도 앞선 기술과 비슷하게 대체재와 보완재의 역할을 수행할 것으로 판단한다. 의료, 금융, 통신 등 이미 인공지능을 도입하고 있는 곳도 비슷한 양상일 것이다. 물론 골드만삭스가 트레이딩 데스크를 모두 IT 인프라로 갈아엎었다는 기사가 났으나, 이것이 성공적이라는 판단은 아직 섣부르다. 이미 잘 나가는 '켄쇼'의 경우 머신러닝으로 데이터를 분석하고 리포팅하는 것이지 시장을 예측해 직접 투자에 나서는 것은 아니다.
인공지능은 사람이 할 수 있는 분석보다 더 많은 양의 분석을 수행함으로써 최종 결정을 더 탄탄하게 만들어줄 수 있으나 최종 결정권자는 아니다. 최종적으로 인간이 인공지능을 통해 나온 결과와 데이터를 이해하고 본인의 전문 지식과 연결해야한다. 예전의 망치와 못이 지금의 컴퓨터와 인공지능이라는 도구로 바뀌는 것이고, 그 도구로 무엇을 만들지는 결국 개인, 회사의 몫이다.
결론적으로 자신의 현 분야의 전문성이 뛰어나고 다른 분야와 연결시켜보는 것을 좋아하는 사람이 주도권을 쥘 것이다. 그런데 이상하지 않은가? 이미 이런 사람들은 예전부터 성공가도를 달렸다. 결국 성공하는 인재상은 크게 달라질 것이 없다.
3줄 요약)
1) 인공지능 많이 발전 해 도구의 위치까지 오고있음
2) 없어지는 직업도 생기는 직업도 있는데, 이는 이미 예전에도 그랬음
3) 그래도 어차피 될놈 될
뉴럴네트워크를 위시한 인공지능 알고리즘은 1943년 처음 모형이 등장했고, 1980년대 연결주의란 이름으로 뇌의 뉴런 연결을 모형화하기 이른다. 하지만 지금에 비하면 조악한 컴퓨팅 파워로 인해 큰 발전을 하지못했고, 2000년대 중반까지도 발전이 더딘 분야였다. 하지만 컴퓨터 자체의 연산 능력이 늘어남은 물론, 클라우드 컴퓨팅 모델이 발달하면서 큰 전기가 마련된다. 특히 클라우드 컴퓨팅은 저렴한 비용으로 고성능 서버의 묶음을 사용하게 한다. 그럼으로써 비용만 충분히 지불한다면 거의 원하는만큼의 컴퓨터를 이용하여 뉴런의 연결을 표현할 수 있다. 그로인해 더 다양한 알고리즘이 등장한다. 특히 2010년경 발표된 'Recursive Neural Network'은 자연어, 시계열 등의 처리에 있어 획기적인 전기를 마련한다. 게다가 구글에서 발표한 'Tensorflow'와 이를 쉽게 사용하기 위한 API까지 등장해 사용자 접근성 또한 획기적으로 높아졌다.
이런 큰 발전에 힘입어 일반 사용자들도 그 혜택을 보기 시작했다. 개인이 집에 둘 수 있는 인공지능 스피커가 있다. 이 스피커는 사용자의 말을 받아들여 연결되어있는 서버에서 답변을 처리해 사용자에게 돌려준다. 아x존의 에x, SxT의 누x 등이 있다. 스마트폰은 이미 S사와 A사가 모두 인공지능 비서를 내부에 탑재하고 있다. 그 외에 바둑을 스포츠로 삼는 동아시아권에서 구x 알파고의 승전보는 매우 큰 충격을 안겨주었다. 이렇다 보니 각종 매체에서 인공지능으로 대체될 직업의 이야기가 심심치않게 보이고, 마치 터x네이터2에서 보던 종말이 다가온 것이 아닌가 하는 영화적 걱정도 보인다.
내 의견은 그런 걱정이 너무 지나치다는 것이다. 인공지능의 사용 추세를 보면 이미 변혁을 일으키기 위한 임계치 근처에 와 있다는 판단은 든다. 이미 사람들이 알게 모르게 인공지능을 접하고 있고, 많은 산업이 인공지능을 도입하여 생산성을 높이려 하고있다. 아마 조금의 시간이 지나면 스마트폰이나 인터넷이 그랬듯이 인공지능도 당당하게 필수 도구의 한 자리를 차지할 것이다. 그렇다면 인터넷과 스마트폰에 빗대어 앞으로를 예상해볼 수 있을 것 같다.
스마트폰이나 인터넷이 등장하고 기술이 발전하면서 사라지거나 힘이 약해진 직업들이 있다. 전화 교환원, 타자를 대신 쳐주던 타자원, 인쇄에 꼭 필요하던 식자공 등이 있다. 하지만 그에 반해 생긴 직업도 있다. 각 회사마다 상주하는 네트워크 관리를 하는 사람, 스마트폰을 파는 사람, 스마트폰 어플리케이션을 개발하는 사람 등 다양하다. 즉, 기술의 발전이 단순히 파괴적 상황만을 가져왔다고 보기 힘들다는 이야기다.
아직 어떤 방향으로 흐를지 정확히 예측하긴 어려우나, 인공지능도 앞선 기술과 비슷하게 대체재와 보완재의 역할을 수행할 것으로 판단한다. 의료, 금융, 통신 등 이미 인공지능을 도입하고 있는 곳도 비슷한 양상일 것이다. 물론 골드만삭스가 트레이딩 데스크를 모두 IT 인프라로 갈아엎었다는 기사가 났으나, 이것이 성공적이라는 판단은 아직 섣부르다. 이미 잘 나가는 '켄쇼'의 경우 머신러닝으로 데이터를 분석하고 리포팅하는 것이지 시장을 예측해 직접 투자에 나서는 것은 아니다.
인공지능은 사람이 할 수 있는 분석보다 더 많은 양의 분석을 수행함으로써 최종 결정을 더 탄탄하게 만들어줄 수 있으나 최종 결정권자는 아니다. 최종적으로 인간이 인공지능을 통해 나온 결과와 데이터를 이해하고 본인의 전문 지식과 연결해야한다. 예전의 망치와 못이 지금의 컴퓨터와 인공지능이라는 도구로 바뀌는 것이고, 그 도구로 무엇을 만들지는 결국 개인, 회사의 몫이다.
결론적으로 자신의 현 분야의 전문성이 뛰어나고 다른 분야와 연결시켜보는 것을 좋아하는 사람이 주도권을 쥘 것이다. 그런데 이상하지 않은가? 이미 이런 사람들은 예전부터 성공가도를 달렸다. 결국 성공하는 인재상은 크게 달라질 것이 없다.
3줄 요약)
1) 인공지능 많이 발전 해 도구의 위치까지 오고있음
2) 없어지는 직업도 생기는 직업도 있는데, 이는 이미 예전에도 그랬음
3) 그래도 어차피 될놈 될
6. Auto-regressive Moving Average 모형
이 포스트에서는 p차 Auto-regressive(AR)와 q차 Moving Average(MA) 모형을 다룬다. 그리고 이 두 모형을 조합한 (p, q)차 ARMA(Auto-regressive, Moving Average) 모형을 소개한다.
앞선 포스트에서 어떤 시계열의 평균이 시간 간격에 상관없이 같은 값이고, 공분산이 시간 간격의 함수로 나타난다면, 그 시계열이 안정적이다라고 정의하였다. 이러한 조건의 안정성을 '약한 안정성(weak stationarity)'라 한다. 여기서는 '엄격한 안정성(strict stationarity)' 조건을 제시한다.
Strict Stationarity - 어떤 시계열 모형 $\{ x_t \}$가 있을 때, 모든 $t_i$와 $m$에 대해 $x_1, \dots , x_{t_n}$과 $x_{t_1 + m}, \dots , x_{t_n + m}$의 joint distribution이 같은 경우, 이 시계열이 strict stationary라고 한다.
시계열 모형을 선택하는데 있어 어떠한 지표가 될만한 값이 있으면 편할 것이다. 그 지표를 제시해주는 것이 이 AIC 값이다. AIC 값은 다음의 식으로 산출한다.
$$
AIC = -2\log(L) + 2k
$$
여기서 $L$은 likelihood 값의 최대치이고, $k$는 모형을 구성하는 인수의 갯수이다. 모형 자체를 선택하거나 모형 내에서 인수의 갯수를 선택할 때, 이 값이 작은 방향으로 선택한다. 즉, likelihood를 크게하고 인수를 적게 쓰는 방향으로 모형 선택을 하는 것이다.
BIC(Bayesian Information Criterion)는 AIC와 유사하며 다음과 같은 식으로 표현한다.
$$
BIC = -2\log(L) + k\log(n)
$$
여기서 $n$은 시계열의 데이터 수를 말한다. 이 값 역시 값이 작아지는 방향으로 모형을 선택한다.
'p'의 차수를 갖는 Auto-regressive 모형은 AR(p)라고 쓰며 다음의 식으로 표현한다.
$$
x_t = \alpha_1 x_{t-1} + \dots + \alpha_{p}x_{t-p} + \omega_t \\
= \sum^{p}_{i=1} \alpha_i x_{t-i} + \omega_t
$$
여기서 $\{\omega_t \}$는 white noise이다.
이를 위해 우선 AR(p) 모형을 backward shift operator의 식 $\theta$로 표현한다. 그 식은 다음과 같다.
$$
\theta_p (\mathbf{B}) x_t = (1 - \alpha_1 \mathbf{B} - \alpha_2 \mathbf{B}^2 - \dots - \alpha_p \mathbf{B}^p)x_t = \omega_t
$$
여기서 다음의 식을 $\mathbf{B}$에 대해 푼다고 하자.
$$
\theta_p (\mathbf{B}) = 0
$$
그렇다면 $\mathbf{B}$의 해를 구할 수 있을 것이다. 이 해의 값이 1인 경우 안정적이지 않고, 1이 아니라면 안정적인 시계열을 갖는다. 이 부분은 특성 함수(characteristic function)에 대한 이해가 필요해 추후 다시 정리를 해보겠다.
$$
\mu_x = E(x_t) = 0 \\
\gamma_k = \sum^p_{i=1} \alpha_i \gamma_{k-i}, k > 0 \\
\rho_k = \sum^p_{i=1} \alpha_i \rho_{k-i}, k > 0
$$
'q' 차수를 갖는 Moving average 모형은 MA(q)로 쓰며 다음의 식으로 표현한다.
$$
x_t = \omega_t + \beta_1 \omega_{t-1} + \dots + \beta_q \omega_{t-q}
$$
Moving average 모형은 white noise 항의 평균으로 시계열을 표현하는 방법이다. 이 white noise는 평균이 0이며 분산이 $\sigma^2$이다. 이 식을 back-shift operator의 함수 $\phi$로 나타내면 다음과 같다.
$$
x_t = (1 + \beta_1 \mathbf{B} + \beta_2 \mathbf{B}^2 + \dots + \beta_q \mathbf{B}^q)\omega_t = \phi_q(\mathbf{B})\omega_t
$$
$$
\mu_x = 0 \\
Var(x) = \sigma^2_{\omega} (1 + \mathbf{B}^2_1 + \dots + \mathbf{B}^2_q) \\
\rho_k = \left\{ \begin{array} \\ 1 & \text{if}\quad k = 0 \\
\sum_{i=0}^{q-k}\beta_i \beta_{i+k} / \sum^q_{i=0} \beta^2_i & \text{if}\quad k = 1, \dots, q\\
0 & \text{if}\quad k>q \end{array} \right.
$$
여기서 $\beta_0 = 1$이다.
ARMA(p, q) 모형은 AR모형과 MA모형을 붙인 형태이다. 이 모형은 이전 시계열의 값과 현 시점에 누적된 white noise를 모두 고려하여 더 유연하게 시계열을 표현할 수 있다. ARMA(p, q)는 다음과 같은 식으로 표현한다.
$$
x_t = \sum^{p}_{i=1} \alpha_i x_{t-i} + \sum^{q}_{j=0} \beta_j \omega_{t-j}
$$
여기서 $\beta_0 = 1$이다.
위의 식을 앞서 제시한 AR과 MA의 back-shift operator의 함수로 나타내면 다음과 같다.
$$
\theta_p (\mathbf{B})x_t = \phi_q (\mathbf{B}) \omega_t
$$
이 모형의 차수인 p와 q를 알맞게 구하기 위해 AIC나 BIC 등의 값을 구한다. 이 작업을 반복하여 AIC, BIC 값이 작아지는 방향으로 차수를 선택한다.
1. 엄격한 안정성(strict stationarity)
앞선 포스트에서 어떤 시계열의 평균이 시간 간격에 상관없이 같은 값이고, 공분산이 시간 간격의 함수로 나타난다면, 그 시계열이 안정적이다라고 정의하였다. 이러한 조건의 안정성을 '약한 안정성(weak stationarity)'라 한다. 여기서는 '엄격한 안정성(strict stationarity)' 조건을 제시한다.
Strict Stationarity - 어떤 시계열 모형 $\{ x_t \}$가 있을 때, 모든 $t_i$와 $m$에 대해 $x_1, \dots , x_{t_n}$과 $x_{t_1 + m}, \dots , x_{t_n + m}$의 joint distribution이 같은 경우, 이 시계열이 strict stationary라고 한다.
2. AIC(Akaike Information Crietrion)와 BIC(Bayesian Information Criterion)
시계열 모형을 선택하는데 있어 어떠한 지표가 될만한 값이 있으면 편할 것이다. 그 지표를 제시해주는 것이 이 AIC 값이다. AIC 값은 다음의 식으로 산출한다.
$$
AIC = -2\log(L) + 2k
$$
여기서 $L$은 likelihood 값의 최대치이고, $k$는 모형을 구성하는 인수의 갯수이다. 모형 자체를 선택하거나 모형 내에서 인수의 갯수를 선택할 때, 이 값이 작은 방향으로 선택한다. 즉, likelihood를 크게하고 인수를 적게 쓰는 방향으로 모형 선택을 하는 것이다.
BIC(Bayesian Information Criterion)는 AIC와 유사하며 다음과 같은 식으로 표현한다.
$$
BIC = -2\log(L) + k\log(n)
$$
여기서 $n$은 시계열의 데이터 수를 말한다. 이 값 역시 값이 작아지는 방향으로 모형을 선택한다.
3. Auto-regressive(AR) 모형
'p'의 차수를 갖는 Auto-regressive 모형은 AR(p)라고 쓰며 다음의 식으로 표현한다.
$$
x_t = \alpha_1 x_{t-1} + \dots + \alpha_{p}x_{t-p} + \omega_t \\
= \sum^{p}_{i=1} \alpha_i x_{t-i} + \omega_t
$$
여기서 $\{\omega_t \}$는 white noise이다.
3.1 AR(p) 모형의 안정성
AR(p) 모형의 안정성은 인수 $\alpha$의 값에 따라 달라진다.이를 위해 우선 AR(p) 모형을 backward shift operator의 식 $\theta$로 표현한다. 그 식은 다음과 같다.
$$
\theta_p (\mathbf{B}) x_t = (1 - \alpha_1 \mathbf{B} - \alpha_2 \mathbf{B}^2 - \dots - \alpha_p \mathbf{B}^p)x_t = \omega_t
$$
여기서 다음의 식을 $\mathbf{B}$에 대해 푼다고 하자.
$$
\theta_p (\mathbf{B}) = 0
$$
그렇다면 $\mathbf{B}$의 해를 구할 수 있을 것이다. 이 해의 값이 1인 경우 안정적이지 않고, 1이 아니라면 안정적인 시계열을 갖는다. 이 부분은 특성 함수(characteristic function)에 대한 이해가 필요해 추후 다시 정리를 해보겠다.
3.2 이차 특성(Second-order properties)
AR(p) 모형의 이차 특성은 다음과 같다.$$
\mu_x = E(x_t) = 0 \\
\gamma_k = \sum^p_{i=1} \alpha_i \gamma_{k-i}, k > 0 \\
\rho_k = \sum^p_{i=1} \alpha_i \rho_{k-i}, k > 0
$$
4. Moving Average 모형
'q' 차수를 갖는 Moving average 모형은 MA(q)로 쓰며 다음의 식으로 표현한다.
$$
x_t = \omega_t + \beta_1 \omega_{t-1} + \dots + \beta_q \omega_{t-q}
$$
Moving average 모형은 white noise 항의 평균으로 시계열을 표현하는 방법이다. 이 white noise는 평균이 0이며 분산이 $\sigma^2$이다. 이 식을 back-shift operator의 함수 $\phi$로 나타내면 다음과 같다.
$$
x_t = (1 + \beta_1 \mathbf{B} + \beta_2 \mathbf{B}^2 + \dots + \beta_q \mathbf{B}^q)\omega_t = \phi_q(\mathbf{B})\omega_t
$$
4.1 이차 특성
이 모형의 이차 특성은 다음과 같다.$$
\mu_x = 0 \\
Var(x) = \sigma^2_{\omega} (1 + \mathbf{B}^2_1 + \dots + \mathbf{B}^2_q) \\
\rho_k = \left\{ \begin{array} \\ 1 & \text{if}\quad k = 0 \\
\sum_{i=0}^{q-k}\beta_i \beta_{i+k} / \sum^q_{i=0} \beta^2_i & \text{if}\quad k = 1, \dots, q\\
0 & \text{if}\quad k>q \end{array} \right.
$$
여기서 $\beta_0 = 1$이다.
5. ARMA(p, q)
ARMA(p, q) 모형은 AR모형과 MA모형을 붙인 형태이다. 이 모형은 이전 시계열의 값과 현 시점에 누적된 white noise를 모두 고려하여 더 유연하게 시계열을 표현할 수 있다. ARMA(p, q)는 다음과 같은 식으로 표현한다.
$$
x_t = \sum^{p}_{i=1} \alpha_i x_{t-i} + \sum^{q}_{j=0} \beta_j \omega_{t-j}
$$
여기서 $\beta_0 = 1$이다.
위의 식을 앞서 제시한 AR과 MA의 back-shift operator의 함수로 나타내면 다음과 같다.
$$
\theta_p (\mathbf{B})x_t = \phi_q (\mathbf{B}) \omega_t
$$
이 모형의 차수인 p와 q를 알맞게 구하기 위해 AIC나 BIC 등의 값을 구한다. 이 작업을 반복하여 AIC, BIC 값이 작아지는 방향으로 차수를 선택한다.
5. 시계열 모형, Random Walks와 White Noise
1. 시계열 모형을 다루는 과정
시계열 모형은 시계열에 있는 serial correlation을 설명하기위한 수학모형이다. 여기서 설명한다는 의미는 다음과 같다. 일단 지정한 모형을 시계열에 맞추면(fitting), correlogram에서 보이는 해당 시계열의 serial correlation을 대부분 설명할 수 있어야 한다.
모형을 선택하고 맞춰가는 과정은 다음과 같이 요약할 수 있다.
- 특정 시계열과 그 움직임에 대한 가설의 윤곽을 잡는다
- R 등의 도구를 이용하여 해당 시계열의 correlogram을 그려본다.
- 오류항(residuals)의 serial correlation을 줄이는 모형을 찾아 맞춘다
- 반복적으로 serial correlation을 없애는 방향으로 맞춰보고 통계 테스트를 수행한다
- 모형과 모형의 'second-order properties'를 이용하여 미래값을 예측한다.
- 예측의 정확도가 최적일 때까지 반복한다.
여기서 'second-order properties'는 앞 포스트에서 얘기한 평균, 분산, serial correlation의 특성을 지칭한다.
모형을 설명하기에 앞서 두 가지 연산자를 소개하고 넘어가려 한다.
- Backward shift operator (lag operator) - $\mathbf{B}$로 표현하며 $\mathbf{B}x_t = x_{t-1}$이다. 반복 적용하면 $\mathbf{B}^n x_t = x_{t-n}$이 된다.
- Difference operator - 표현은 $\nabla$로 한다. 라플라스 연산자(Laplace operator)와 같은 모양인데, 이 책에서는 difference로 사용한다. $\nabla x_t = x_t - x_{t-1}$ 또는 $\nabla x_t = (1-\mathbf{B})x_t$이다.
2. White Noise
White noise 모형은 방향성이 없는 모형이며, 주로 오류항의 시계열을 나타내기위해 사용한다. $y_t$가 관찰한 값의 시계열이고, $\hat{y}_t$가 예측치라면, 오류항의 시계열 $x_t$는 $y_t - \hat{y}_t$이다.
만약 적당한 시계열 모형을 선택했다면, 모형으로 측정한 값과 실측값의 차이(오류 시계열)의 serial correlation은 거의 없게 된다. 즉, 오류 자체가 white noise로서 서로 독립적인 값이 되므로 새로운 모형을 적용할 여지가 없어진다.
White noise의 second-order properties는 다음과 같다.
$$ \begin{eqnarray}
& \mu_{\omega} = \mathbf{E}(\omega_t) = 0 \\
& \rho_k = \mathbf{Cor}(\omega_t, \omega_{t+k}) =
\left\{ \begin{array} \\
1, k = 0 \\
0, k \not= 0
\end{array} \right. \end{eqnarray}
$$
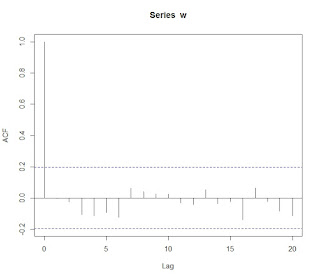
그리고 correlogram은 다음과 같이 나타난다.
Random walk 시계열 모형은 직전 시계열 값에 오류항을 더한 식으로 표현한다.
$$
x_t = \mathbf{B}x_t + \omega_t = x_{t-1} + \omega_t
$$
위의 식을 반복하여 적용하면 다음과 같은 식을 얻을 수 있다.
$$
x_t = (1 + \mathbf{B} + \mathbf{B}^2 + \dots )\omega_t \Longrightarrow x_t = \sum_{i=0}^n \omega_{t-i}
$$
즉, random walk는 서로 독립인 오류항의 합으로 나타난다.
오류항의 분산이 $\sigma^2$라고 하면, random walk의 second-order properties는 다음과 같다.
$$
\begin{eqnarray}
&\mu_x = 0 \\
&\gamma_k(t) = \mathbf{Cov}(x_t, x_{t+k}) = t\sigma^2 \\
&\rho_k(t) = \frac{\mathbf{Cov}(x_t, x_{t+k})}{\sqrt{\mathbf{Var}(x_t)\mathbf{Var}(x_{t+k})}} = \frac{t\sigma^2}{\sqrt{t\sigma^2(t+k)\sigma^2}} = \frac{1}{\sqrt{1+k/t}} \end{eqnarray}
$$
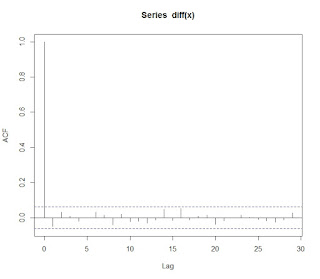
위의 식에서 볼 수 있듯이, random walk의 공분산이 $k$가 아닌 $t$의 함수이다. 그러므로 random walk는 non-stationary 시계열 모형이다. 이 모형의 correlogram은 다음과 같다.
$\nabla x_t = x_t - x_{t-1}$의 correlogram을 그려본다. 이 작업은 random walk로 생성한 데이터를 random walk 모형으로 추정했다고 가정했을 때, 오류항의 serial correlation을 볼 수 있는 작업이다.
& \mu_{\omega} = \mathbf{E}(\omega_t) = 0 \\
& \rho_k = \mathbf{Cor}(\omega_t, \omega_{t+k}) =
\left\{ \begin{array} \\
1, k = 0 \\
0, k \not= 0
\end{array} \right. \end{eqnarray}
$$
그리고 correlogram은 다음과 같이 나타난다.
3. Random Walk
Random walk 시계열 모형은 직전 시계열 값에 오류항을 더한 식으로 표현한다.
$$
x_t = \mathbf{B}x_t + \omega_t = x_{t-1} + \omega_t
$$
위의 식을 반복하여 적용하면 다음과 같은 식을 얻을 수 있다.
$$
x_t = (1 + \mathbf{B} + \mathbf{B}^2 + \dots )\omega_t \Longrightarrow x_t = \sum_{i=0}^n \omega_{t-i}
$$
즉, random walk는 서로 독립인 오류항의 합으로 나타난다.
오류항의 분산이 $\sigma^2$라고 하면, random walk의 second-order properties는 다음과 같다.
$$
\begin{eqnarray}
&\mu_x = 0 \\
&\gamma_k(t) = \mathbf{Cov}(x_t, x_{t+k}) = t\sigma^2 \\
&\rho_k(t) = \frac{\mathbf{Cov}(x_t, x_{t+k})}{\sqrt{\mathbf{Var}(x_t)\mathbf{Var}(x_{t+k})}} = \frac{t\sigma^2}{\sqrt{t\sigma^2(t+k)\sigma^2}} = \frac{1}{\sqrt{1+k/t}} \end{eqnarray}
$$
위의 식에서 볼 수 있듯이, random walk의 공분산이 $k$가 아닌 $t$의 함수이다. 그러므로 random walk는 non-stationary 시계열 모형이다. 이 모형의 correlogram은 다음과 같다.
$\nabla x_t = x_t - x_{t-1}$의 correlogram을 그려본다. 이 작업은 random walk로 생성한 데이터를 random walk 모형으로 추정했다고 가정했을 때, 오류항의 serial correlation을 볼 수 있는 작업이다.
4. 시계열 분석과 Serial Correlation
1. 시계열 분석
시계열이란 시간 순서대로 관찰한 어떠한 값의 모음을 이야기한다. 어떤 주가 지수의 종가를 날짜별로 나열한 값이나, 시점에 따른 직장인 평균 월급을 모아놓은 값 등이 예제가 될 수 있다.
시계열 분석은 이 데이터를 가지고 어떤 일이 일었났는가를 추론한다. 그리고 그 추론을 바탕으로 미래값을 예측하는 방법이다.
일반적으로 시계열은 다음과 같은 특성을 지닌다.
- Trend - trend는 시계열이 지니고 있는 방향성을 의미한다. 방향성은 deterministic할 수도 있고, stochastic할 수도 있다.
- Seasonal Variation - 주기에 따른 시계열의 변화를 의미한다. 예를들어 천연가스의 사용량은 계절에 따라 주기성을 보인다.
- Serial Dependence - 시계열의 시간에 따른 관찰 결과가 어떤 상관관계를 갖을 수 있다. 금융 시계열 분석에서 매우 중요하게 생각하는 serial correlation으로 나타낸다.
2. 시계열의 Stationarity
Stationarity는 시계열 분석에 있어 중요한 부분을 차지한다. 많은 금융 데이터 시계열분석이 stationarity를 염두해두고 수행된다. 시계열의 stationarity를 이야기하기 위해서 시계열의 expectation(기대값)과 variance(분산)을 이야기해야 한다.
우선 시계열 $x_t$의 기대값(평균)은 $t$의 함수인 $\mu(t)$로 나타내며, $\mathbf{E}(x_t)=\mu(t)$로 표현한다. 평균, 분산 등을 구하기 위한 시계열이 여러개일 수 있지만, 일반적으로 하나의 시계열을 가지고 작업하는 경우가 많다. 시계열이 하나라면, 평균을 구하기위해 다음의 두가지 방법을 고려할 수 있다.
- 관찰한 데이터를 바탕으로 각 점에서 단순히 평균을 구하는 방법
- 시계열 데이터에서 trend, seasonality 효과를 제거하여 residual series를 만든다. 이 경우 만들어진 residual series가 stationarity in the mean(안정적 평균) 상태임을 가정할 수 있다. 그래서 상수의 $\bar{x} = \sum^{n}_{t=1} x_t/n$로 평균을 추정한다.
앞서 'stationarity in the mean'은 $\mu(t) = \mu$를 의미한다. 즉, 시계열이 시간에 관계없이 항상 동일한 평균을 갖는다는 의미이다. 시계열이 이 상태라면 분산을 다음과 같이 구한다.
$$
\sigma^2 = \mathbf{E}[(x_t - \mu)^{2}]
$$
\sigma^2 = \mathbf{E}[(x_t - \mu)^{2}]
$$
이 때 역시 시계열이 하나밖에 없을 경우, 분산이 시간에 관계없이 일정하다고 가정하고 sample variance를 구하는 방법이 있다.
$$
\mathbf{Var}(x) = \frac{\sum(x_t - \bar{x})^2}{n-1}
$$
이 경우 이 시계열을 stationarity in the variance(안정적 분산) 상태라고 부른다.
Serial correlation을 위해 우선 lag라는 개념을 보자. Lag는 하나의 전체 시계열이 있을 때 시간 차를 두고 추출한 하위 시계열이다. 예를 들어 시계열 $\vec{x}_{t} = \{x_t, x_{t-1}, x_{t-2} ... x_{0}\}$가 있다고 하자. 여기서 lag이 1일 때 시계열은 $\vec{x}_{t+1} = \{x_{t+1}, x_{t}, x_{t-1} ... x_{1}\}$이 된다.
이렇게 lag를 건너 뛴 시계열도 하나의 또 다른 시계열로 볼 수 있다. 그래서 두 시계열간의 상관관계가 존재한다. 이 때 이 상관관계가 $t$의 함수가 아니라 lag를 의미하는 $k$의 함수로 나타낼 수 있다면, 이런 경우를 'Second order stationary'상태라 한다.
시계열이 second order stationary 상태라면, 두 시계열간 공분산(autocovariance)을 다음과 같이 구할 수 있다.
$$
C_k = \mathbf{E}[(x_t - \mu)(x_{x+k} - \mu)]
$$
잘 보면 이 second order stationary가 앞서 이야기한 mean, variance의 stationary를 포함하는 것으로 볼 수 있다.
이렇게 구해진 autocovariance를 이용하여 serial correlation(autucorrelation)을 다음과 같이 구할 수 있다.
$$
\rho_k = \frac{C_k}{\sigma^2}
$$
다음의 차트는 100개의 난수로 이루어진 시계열의 correlogram(lag별 autocorrelation 차트)이다.
난수의 시계열이므로 lag가 0인경우만 serial correlation이 1이고 나머지는 거의 0에 수렴한다.
다음은 1부터 100까지의 수열에 대한 차트이다.
Lag값이 커질수록 값이 줄어들지만, 전반적으로 높은 수준의 상관관계를 보여준다.
마지막으로 반족되는 수열의 차트이다.
차트에서 보듯이 반복 주기마다 상관계수가 높아지는 것을 확인할 수있다.
$$
\mathbf{Var}(x) = \frac{\sum(x_t - \bar{x})^2}{n-1}
$$
이 경우 이 시계열을 stationarity in the variance(안정적 분산) 상태라고 부른다.
3. Serial Correlation
Serial correlation을 위해 우선 lag라는 개념을 보자. Lag는 하나의 전체 시계열이 있을 때 시간 차를 두고 추출한 하위 시계열이다. 예를 들어 시계열 $\vec{x}_{t} = \{x_t, x_{t-1}, x_{t-2} ... x_{0}\}$가 있다고 하자. 여기서 lag이 1일 때 시계열은 $\vec{x}_{t+1} = \{x_{t+1}, x_{t}, x_{t-1} ... x_{1}\}$이 된다.
이렇게 lag를 건너 뛴 시계열도 하나의 또 다른 시계열로 볼 수 있다. 그래서 두 시계열간의 상관관계가 존재한다. 이 때 이 상관관계가 $t$의 함수가 아니라 lag를 의미하는 $k$의 함수로 나타낼 수 있다면, 이런 경우를 'Second order stationary'상태라 한다.
시계열이 second order stationary 상태라면, 두 시계열간 공분산(autocovariance)을 다음과 같이 구할 수 있다.
$$
C_k = \mathbf{E}[(x_t - \mu)(x_{x+k} - \mu)]
$$
잘 보면 이 second order stationary가 앞서 이야기한 mean, variance의 stationary를 포함하는 것으로 볼 수 있다.
이렇게 구해진 autocovariance를 이용하여 serial correlation(autucorrelation)을 다음과 같이 구할 수 있다.
$$
\rho_k = \frac{C_k}{\sigma^2}
$$
4. 예제
다음의 차트는 100개의 난수로 이루어진 시계열의 correlogram(lag별 autocorrelation 차트)이다.
난수의 시계열이므로 lag가 0인경우만 serial correlation이 1이고 나머지는 거의 0에 수렴한다.
다음은 1부터 100까지의 수열에 대한 차트이다.
Lag값이 커질수록 값이 줄어들지만, 전반적으로 높은 수준의 상관관계를 보여준다.
마지막으로 반족되는 수열의 차트이다.
차트에서 보듯이 반복 주기마다 상관계수가 높아지는 것을 확인할 수있다.
잡설 - 이상한 꿈
이상한 꿈을 꾸었다.
나는 나도 모르는 사이 이 세상 사람이 아니었다. 그 사실을 알게된 것은 약간의 시간이 지나서였다. 나름 하루 일과를 마치고 거리를 걷고있는데 이상한 느낌이 들었다. 어딘가에 부딪힌 것 같은데 아무 느낌이 없었다.
집으로 돌아왔다. 분명 내가 살던 집인데 낯설었다. 와이프는 말 없이 음식을 준비하고 있었고, 아들은 여느때 처럼 거실에서 스케치북에 그림을 그리고 있었다. 그 때 아들이 아빠가 보고싶다며 엄마에게 칭얼거렸다. 엄마는 잠시 멈칫하다 하던 일을 다시했고, 나는 그 모습을 가만히 보고있었다. 와이프의 뺨을 만져봤지만 내 손에 느껴지는 감각이 약했다. 그리고 와이프도 아무런 반응이 없었다. 평소같으면 집에 돌아온 아빠에게 안겼을 아이들이 내 옆을 지나쳐간다.
시간 개념이 뚜렷치 않아 꽤 시일이 지난 후 같다. 비가 오고 있었다. 빗속을 비에 젖지 않은체 걸었다. 비가 그치고 해가 났을 때, 누군가와 이야기를 나누었다. 누구인지 보지 않고 이야기를 나누었다. 이제 내 상황을 알았으니 체념하겠다. 이런식으로 지내는 것도 나쁘지 않다라는 내용이었다. 그 때, 갑자기 혼자 남은 와이프와 앞으로 아빠를 잊어갈 아이들이 생각났다. 그리고 내가 왜 죽음으로 내몰렸는지(아마도 어이없이 살해당했던 것으로 기억한다.)도 기억이 나기 시작했다. 원망스러움과 안타까움, 슬픔, 그 외 수 많은 감정이 파도처럼 밀려왔고, 나는 그 자리에 주저앉아 큰 소리로 울었다. 어차피 누구도 우는 소리를 못 들을테니까.
그렇게 우는 장면을 마지막으로 꿈에서 깼다. 잠에서 깬 직후의 멍멍함과 꿈속에서의 감각이 남아 베개에 얼굴을 파묻고 잠시 있었다. 시계를 보니 알람이 울리기 30분 전이었다. 아이들과 와이프가 자고있는 방으로 가 그들을 바라보니 다시 현실임을 자각했다. 마지막 장면의 강렬함 때문이었을까. 문득 이렇게 현실에서 살아있는게 다행이라는 생각이 들었다.
참 이상한 꿈이었다.
나는 나도 모르는 사이 이 세상 사람이 아니었다. 그 사실을 알게된 것은 약간의 시간이 지나서였다. 나름 하루 일과를 마치고 거리를 걷고있는데 이상한 느낌이 들었다. 어딘가에 부딪힌 것 같은데 아무 느낌이 없었다.
집으로 돌아왔다. 분명 내가 살던 집인데 낯설었다. 와이프는 말 없이 음식을 준비하고 있었고, 아들은 여느때 처럼 거실에서 스케치북에 그림을 그리고 있었다. 그 때 아들이 아빠가 보고싶다며 엄마에게 칭얼거렸다. 엄마는 잠시 멈칫하다 하던 일을 다시했고, 나는 그 모습을 가만히 보고있었다. 와이프의 뺨을 만져봤지만 내 손에 느껴지는 감각이 약했다. 그리고 와이프도 아무런 반응이 없었다. 평소같으면 집에 돌아온 아빠에게 안겼을 아이들이 내 옆을 지나쳐간다.
시간 개념이 뚜렷치 않아 꽤 시일이 지난 후 같다. 비가 오고 있었다. 빗속을 비에 젖지 않은체 걸었다. 비가 그치고 해가 났을 때, 누군가와 이야기를 나누었다. 누구인지 보지 않고 이야기를 나누었다. 이제 내 상황을 알았으니 체념하겠다. 이런식으로 지내는 것도 나쁘지 않다라는 내용이었다. 그 때, 갑자기 혼자 남은 와이프와 앞으로 아빠를 잊어갈 아이들이 생각났다. 그리고 내가 왜 죽음으로 내몰렸는지(아마도 어이없이 살해당했던 것으로 기억한다.)도 기억이 나기 시작했다. 원망스러움과 안타까움, 슬픔, 그 외 수 많은 감정이 파도처럼 밀려왔고, 나는 그 자리에 주저앉아 큰 소리로 울었다. 어차피 누구도 우는 소리를 못 들을테니까.
그렇게 우는 장면을 마지막으로 꿈에서 깼다. 잠에서 깬 직후의 멍멍함과 꿈속에서의 감각이 남아 베개에 얼굴을 파묻고 잠시 있었다. 시계를 보니 알람이 울리기 30분 전이었다. 아이들과 와이프가 자고있는 방으로 가 그들을 바라보니 다시 현실임을 자각했다. 마지막 장면의 강렬함 때문이었을까. 문득 이렇게 현실에서 살아있는게 다행이라는 생각이 들었다.
참 이상한 꿈이었다.
3. Bayesian Linear Regression
1. Frequentist 방식
다음의 예측 식이 있다고 하자.
$$
f(\mathbf{X}) = \beta_0 + \sum_{j=1}^{p}\mathbf{X}_j\beta_j + \epsilon \\
= \beta^T \mathbf{X} + \epsilon
$$
여기서 $\epsilon \sim N(0, \sigma^2)$인 에러텀이다. 여기서 학습을 위한 데이터가 $(x_1, y_1), ...(x_N, y_N)$과 같이 있다고 하면, 우리는 이 데이터를 가장 비슷하게 맞추는 $\beta$를 찾아야 한다. 이를 위해 일반적으로 OLS(ordinary least squares)방식을 사용한다. OLS 방식을 사용하기 위해 우선 측정 값과 $\beta$를 통한 예측치간의 차이를 나타내는 다음의 식을 정의한다.
$$
RSS(\beta) = \sum^{N}_{i=1}(y_i - f(x_i))^2
$$
이 식(RSS: residual sum of squares)는 일종의 비용(에러)함수로 볼 수 있다. OLS의 목적은 이 함수의 값을 최소화하는 $\beta$를 찾는 것이고, 이를 위해 Maximum Likelihood Estimate 방식을 사용한다. 이 식은 다음과 같다.
$$
\hat{\beta} = (\mathbf{X}^T \mathbf{X})^{-1}\mathbf{X}^T \mathbf{y}
$$
이렇게 찾아진 $\hat{\beta}$를 이용하여 $x_{N+1}$ 값에 대한 결과치 $y_{N+1}$을 추정한다.
2. Bayesian 방식
Bayesian 방식으로 Linear Regression을 수행하기 위해 다음과 같이 $\mathbf{y}$에 대해 정의한다.
$$
\mathbf{y} \sim N(\beta^T \mathbf{X}, \sigma^2 \mathbf{I})
$$
즉, 앞서 소개한 방식과 다르게 $y$를 어떤 점으로 보는 것이 아니라, 일종의 확률변수로 보는 것이다. 이를 수행하기 위해 다음의 두 가지를 고려해야 한다.
- Prior Distribution - $\beta$에 대한 선행 정보가 있을 경우, 이를 반영하기 위한 분포를 지정한다. 만약 정보가 없을 경우 'non-informative prior'를 선택한다.
- Posterior Distribution - Bayesian 방식은 $\beta$도 분포를 갖는 확률변수로 취급하므로 데이터 추가에 따른 새로운 $\beta$의 분포를 도출한다.
앞선 포스트에서 설명하였듯이, $\beta$의 분포가 conjugate prior인 경우 닫힌 해를 이용하여 다음 $\beta$의 분포를 추정할 수 있다. 그렇지 않을 경우 일정 분포를 가정하고 Markov Chain Monte Carlo 방법을 이용하여 추정작업을 수행한다.
3. PyMC3를 이용한 Bayesian Linear Regression 예제
너무나도 간단한 설명을 마치고 PyMC3를 이용하는 예제를 소개한다.
3.1 Generalized Linear Model(GLM)
GLM 모형은 일반적인 Linear Regression 모형의 확장형태라고 볼 수 있다. 결과 값으로 나오는 $y$의 오류값이 정규분포가 아닌 다른 분포를 갖을 수 있도록 허용한 방식이다. 자세한 내용은 위키페이지를 참고하기 바란다.GLM 모형은 결과값 $y$가 지수형태를 갖는 특정 분포를 통해 만들어진다고 가정한다. $y$는 다음과 같은 평균값을 갖는다.
$$
\mathbf{E}(\mathbf{y}) = \mu = g^{-1}(\mathbf{X}\beta)
$$
여기서 $\mathbf{X}\beta$가 linear predictor 역학을 하는데, $\beta$가 미지수이다. $g()$는 연결함수(link function)이다. 그리고 분산은 평균의 함수 $V$로 표현한다.
$$
Var(\mathbf{y}) = V(\mathbf{E}(\mathbf{y})) = V(g^{-1}(\mathbf{X}\beta))
$$
이 모형을 가지고 $\beta$를 다양한 방식으로 추정하는데, 여기서는 Markov Chain Mote Carlo를 이용한다.
3.2 수행 예제
다음의 예제는 위의 GLM모형을 임의의 데이터에 적용하는 예제이다. 난수로 만들어진 일정 데이터에 맞게 $\beta$를 찾는 코드이다. 우선 다음의 그림은 frequentist 방식으로 fitting한 결과이다.
이 작업을 MCMC를 이용한 결과는 다음과 같다. 다음의 그림은 5000번의 수행 중, 100개의결과를 임의 추출한 것이다.
위 그림의 녹색선이 목표지점이다. 이 MCMC수행의 추적 차트는 다음과 같다.
위 그림에서 intercept가 $\beta_0$, $x$가 $\beta_1$, sd가 error이다.
이를 수행하는 코드를 다음에 첨부한다.
# simul_fit.py
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
import pymc3 as pm
sns.set(style="darkgrid", palette="muted")
# simulate function
def simulate_linear_data(N, beta_0, beta_1, eps_sigma_sq):
"""
simulate a random dataset using a noisy linear proces
:param N: Number of data points
:param beta_0: Intercept
:param beta_1: slope of univariate predictor, X
:param eps_sigma_sq:
:return: pandas dataframe
"""
# create pandas DataFrame
# column 'x' : N uniformly sampled values b/w 0.0 and 1.0
df = pd.DataFrame(
{ "x":
np.random.RandomState(42).choice(
list(map(
lambda x: float(x) / 100.0,
np.arange(N)
)), N, replace=False
)
}
)
# Use linear model (y ~ beta_0 + beta_1*x + epsilon) to
# generate a column 'y' of responses based on 'x'
eps_mean = 0.0
df["y"] = beta_0 + beta_1 * df["x"] + np.random.RandomState(42).normal(
eps_mean, eps_sigma_sq, N)
return df
def glm_mcmc_inference(df, iterations=5000):
"""
Calculate MCMC trace of GLM
:param df:
:param iterations:
:return:
"""
# use PyMC3 to construct model context
basic_model = pm.Model()
with basic_model:
# create the glm using the Patsy model syntax
# Normal distribution for likelihood
pm.glm.GLM.from_formula("y ~ x", df, family=pm.glm.families.Normal())
# use Maximum A Posterior(MAP) optimization as initial value
start = pm.find_MAP()
# use the No-U-Turn Sampler
step = pm.NUTS()
# Calculate trace
trace = pm.sample(iterations, step, start, random_seed=42, progressbar=True)
return trace
# main
if __name__ == "__main__":
# true parameters
beta_0 = 1.0 # Intercept
beta_1 = 2.0 # Slope
# simulate 100 points
N = 100
eps_sigma_sq = 0.5
# Simulate the linear data
df = simulate_linear_data(N, beta_0, beta_1, eps_sigma_sq)
# plot data, and Frequentist linear regression fit
# using seaborn package
sns.lmplot(x="x", y="y", data=df, size=10)
plt.xlim(0.0, 1.0)
trace = glm_mcmc_inference(df, iterations=5000)
pm.traceplot(trace[500:])
plt.show()
# plot a sample of posterior regression lines
sns.lmplot(x="x", y="y", data=df, size=10, fit_reg=False)
plt.xlim(0.0, 1.0)
plt.ylim(0.0, 4.0)
pm.plot_posterior_predictive_glm(trace, samples=100)
x = np.linspace(0, 1, N)
y = beta_0 + beta_1 * x
plt.plot(x, y, label="True Regression Line", lw=3., c="green")
plt.legend(loc=0)
plt.show()
유시민의 글쓰기 특강(유시민, 2015)

나에게 유시민은 작가라기 보다, 참여정부의 정치인으로서 더 익숙하다. 노무현 대통령 탄핵 표결 당시 분루를 곱씹던 그 날카로운 눈매나, 첫 국회 연설 때 비지니스 캐쥬얼을 입고 나와 욕을 먹던 모습 등이 기억난다.
하지만 유시민은 정치인 이전에 '거꾸로 읽는 세계사' 등을 집필한 작가이다. 그가 처음 세상에 이름을 알린 것은 '서울대 프락치 사건'의 1심 판결 이후 작성한 '항소 이유서'를 통해서이다. 학생 뿐 아니라 심지어 판사들까지 돌려 읽어볼 정도로 날카로움과 절절함을 담고있는 글이었다.
이 책은 유시민 작가가 본인의 글쓰기 노하우를 담아낸 책이다. 글의 큰 틀 부터, 문장, 단어까지 세세히 짚어가며 본인이 생각하는 좋은 글에 대해 논한다.
기억나는 것 중 가장 인상적인 것은, '취향과 주장'에 관한 내용이었다. 취향은 논쟁거리가 아니며 주장은 그를 뒷받침할 논증을 반드시 해야한다는 내용이다. 최근 인터넷을 돌아다니는 글, 심지어 신문 사설마저도 이 내용을 지키지못한 경우가 많다. 찬찬히 읽고있노라면 저자의 분풀이말고는 어떤 내용도 없는 경우가 있고, 그렇다보니 읽는 시간이 아까운 경우가 부지기수다.
다음은 어려운 글이 좋은 것이 아니라 쉽게 쓰여있더라도 내용을 힘있게 담아내는 글이 좋은 글이라는 내용이다. 내가 읽어본 책 중 가장 인상깊었던 책을 꼽으라면 '칼 세이건'의 '코스모스'와 '스티븐 호킹'의 '시간에관한 짧은 역사'이다. 이 두 책에 담겨있는 내용은 결코 쉽지도, 가볍지도 않다. 애초에 전공자가 아니라면 이해하기 힘든 내용이 부지기수다. 하지만 두 책 모두 현학적으로 말을 꼬으거나 어렵게 쓰지 않고 쉬운 단어, 문장으로 썼다는 공통점이 있다. 그렇다보니 깊은 이해는 어렵더라도 책을 계속해서 읽어가는데 무리가 없고, 호기심도 계속 유지가되는 장점이 있다.
마지막으로 이 책에서 꾸준히 강조하는 내용은 많이 읽고, 많이 쓰라는 것이다. 이 책을 읽는동안 계속해서 반복하는 말이다. 그러면 자연스레 좋은 글을 알게되고, 쓰기 근육이 늘어난다는 내용이다.
이 책을 읽고나면 비단 글 쓰는 것만 도움을 받는 것이 아니다. 요즘 시대는 인터넷에 다양한 글이 존재하며, SNS를 통해 다양한 글을 접할 수 있다. 그 글들을 읽었을 때 좋은 글을 구분해 낼 수 있는 기준이 이 책을 통해서 만들어질 수 있다. 글에 관심이 있다면 꼭 한번 읽어볼 책이다.
2. Markov Chain Monte Carlo
1. Bayesian 추론에서 MCMC를 왜 쓰는가?
Markov Chain Monte Carlo는 각각의 시도가 이전 시도에 영향을 받지 않는(memoryless, Markov Chain) 랜덤서치(Monte Carlo)를 통하여 답을 구하는 방식이다.
1번 포스트에서 썼던 예제는 prior belief와 posterior가 같은 형태의 분포를 갖는 conjugate prior형태이므로 닫힌 해를 이용하여 posterior를 구할 수 있었다. 하지만 대부분의 문제는 $\theta$로 표현하는 인수의 수가 많고, conjugate prior가 아닌 경우가 많아 닫힌 해를 이용하기가 힘들다. 다시 한 번 Bayes Rule의 식을 보자.
$$
P(\theta|D)=\frac{P(D|\theta)P(\theta)}{P(D)}
$$
위의 식에서 보면 posterior의 $\theta$를 계산하기 위해서는 $P(D)$를 계산해야 하고, 이를 위해 다음의 적분을 해야 한다.
$$
P(D) = \int_{\Theta} P(D, \theta)d\theta
$$
하지만 인수를 구성하는 $\theta$의 수가 많아질 경우 앞서 설명한대로 닫힌 해를 이용한 적분이 매우 어렵고, 그로인해 닫힌해를 가지고 posterior의 $\theta$를 추정하기가 힘들다.
그러므로 이런 경우 posterior의 $\theta$를 구하기 위해 MCMC를 적용한다. 물론 여기서 위 적분을 직접 구하는 것은 아니다.
2. MCMC 알고리즘
MCMC에 속하는 알고리즘은 다음과 같다. Metropolis, Metropolis-Hastings, Gibbs Sampler, Hamiltonian MCMC, No-U-Turn Sampler(NUTS), 그 외.
이 챕터에서는 가장 오래되고 널리 쓰이는 Metropolis를 우선 설명하고, 이후 챕터에서 다른 알고리즘을 소개한다.
3. Metropolis 알고리즘
일반적으로 MCMC 알고리즘은 다음의 순서를 따른다.
- 현재 인수에서 시작($\theta_{c}$)
- 새로운 인수로의 점프를 제안($\theta_{n}$)
- 이전 정보와 데이터를 이용하여 확률적으로 새로운 인수의 허용/거부를 결정
- 허용을 결정하면 새로운 인수로 업데이트 후 1번부터 반복
- 거부를 결정하면 인수를 업데이트하지 않고 1번부터 반복
- 지정된 횟수만큼의 시도를 한 후 허용을 결정한 인수를 모두 모음
위의 과정에서 '어떻게 점프를 하는가'와 '어떻게 점프 여부(허용/거부)를 결정하는가'가 알고리즘마다 다르다.
Metropolis 알고리즘은 새로운 인수를 찾아 제안할 때, 인수에 대해 가정한 분포와 상관없이 '정규 분포'를 따라 다음 인수를 제안한다. 그래서 다음 제안을 위한 $\mu$와 $\sigma$가 있는데, $\mu$는 기존의 $\theta_{c}$로 정한다. 여기서 $\sigma$를 어찌 지정하는가에 따라 수렴에 영향을 미친다. $\sigma$가 큰 값일 경우 더 넓은 영역을 살펴볼 수 있으나 허용 확률이 높은 부분을 놓치고 지나갈 수 있고, 값이 작을 경우 큰 영역을 살피는데 시간이 오래 걸리므로 수렴 시간이 더 길어질 가능성이 있다.
이렇게 새로운 인수에 대한 제안이 만들어지면 이제 이 제안을 받아들일지 여부를 결정해야 한다. 이를 위해 가정한 $\theta$의 분포에 따라 $P(\theta_{n})$와 Likelihood $P(D|\theta)$를 계산한다. 그리고 다음의 비율을 구한다.
$$p = \frac{ P(D|\theta_{n})P(\theta_{n}) }{ P(D|\theta_{c})P(\theta_{c}) }
$$
그리고 $[0, 1]$에 속하는 균일 분포의 난수를 만들고, 만들어진 수가 $[0, p]$안에 들어오면 이 인수를 허용하고, 아니면 거부한다.
결국 Bayesian 추론에서는 새로운 인수로 만들어진 posterior $P(\theta_{n}|D)$를 시뮬레이션을 통하여 구해가는 과정인 것이다.
실제로 앞서 제시한 Coin toss 문제를 Metropolis를 이용하여 푼 예제를 보자. 여기서 50번의 동전 던지기에서 10번의 앞면이 나왔을 경우 posterior를 구하는 예제이다.
위 그림에서 녹색선으로 그려진 부분이 닫힌 해를 이용한 답이고, 붉은 박스로 그려진 히스토그램이 Metropolis를 이용한 결과이다. 나름 비슷한 모양으로 답을 찾은 것을 볼 수 있다. 하지만 이 시뮬레이션의 경우 $\theta$의 수가 하나인데도, 이 결과를 얻기 위해 십만 번의 시뮬레이션을 수행해야 했다. 그러니 인수의 수가 많아질수록 더 큰 컴퓨팅 파워를 필요로 하게될 것이다.
위 그래프는 PyMC3라는 라이브러리를 이용하여 python으로 구현한 내용이다. 코드를 다음에 첨부한다.
위 그래프는 PyMC3라는 라이브러리를 이용하여 python으로 구현한 내용이다. 코드를 다음에 첨부한다.
# mcmc_coin.py
# Markov Chain Monte Carlo Test for coin flipping
import matplotlib.pyplot as plt
import numpy as np
import pymc3
import scipy.stats as stats
# gg plot style의 plotting
plt.style.use("ggplot")
# parmeters
n = 50 # num of coin flip
z = 10 # num of heads
alpha = 12 # alpha for beta-distribution
beta = 12 # beta for beta-distribution
alpha_post = 22 # known updated parameter
beta_post = 52 # known updated parameter
# Metropolis algorithm에서 수행할 시뮬레이션 횟수
iterations = 100000
# PyMC3를 사용하여 model context 만들기
basic_model = pymc3.Model()
with basic_model:
# Beta Distribution을 이용하여 prior belief 만들기
theta = pymc3.Beta("theta", alpha=alpha, beta=beta)
# Bernoulli likelihood 함수 지정
y = pymc3.Binomial("y", n=n, p=theta, observed=z)
#Metrobpolis Algorithm을 이용하여 MCMC수행
# Maximum A Posteriori (MAP) 최적화를 initial value를 찾는데 사용
start = pymc3.find_MAP()
step = pymc3.Metropolis()
# trace 계산
trace = pymc3.sample(iterations, step, start, random_seed=1, progressbar=True)
# posterio histogram 그리기
bins = 50
plt.hist(trace["theta"], bins, histtype="step", normed=True, label="Posterior (MCMC)", color="red")
# analytic 찍기
x = np.linspace(0, 1, 100)
plt.plot(x, stats.beta.pdf(x, alpha, beta), "--", label="Prior", color="blue")
plt.plot(x, stats.beta.pdf(x, alpha_post, beta_post), label="Posterior (Analytic)", color="green")
#graph label
plt.legend(title="Parameters", loc="best")
plt.xlabel("$\\theta$, Fairness")
plt.ylabel("Density")
plt.show()
MCMC에 관해 조금 더 쉽게 설명된 내용은 http://twiecki.github.io/blog/2015/11/10/mcmc-sampling/ 를 참고하기 바란다.
1. Bayesian Statistics와 Coin toss
0. 앞으로 Michael L. Halls-Moore의 'Advanced Algorithmic Trading'을 스터디하며 요약 정리를 해 볼 심산이다. 처음으로 Bayesian Statistics와 그 예로 항상 등장하는 Coin toss 문제를 책에 제시한 내용을 가지고 요약해보겠다.
통계 문제에 확률을 적용하는 방법은 크게 'Bayesian'과 'Frequentist'가 있다. 'Frequentist'는 확률이란 어느 사건이 아주 많은 수의 수행 속에 나타난 빈도라고 생각하는 것이다. 그래서 이 경우 ideal 확률을 알아야 하며, 이 값이 변하지 않는다.
'Bayesian'의 경우, 이미 일어난 사건(data)와 앞으로 일어날 사건을 바탕으로 우리가 믿고있는 확률을 변화시킬 수 있다고 한다.
최근 이슈가되는 Machine Learning이나, 예전부터 많이 사용되는 Time Series Analysis는 모두 Bayesian Statistics에 바탕을두고있다.
Bayes' Rule은 조건부 확률(conditional probability), 즉, 'B라는 일이 일어났을 때 A라는 일이 일어날 확률은 얼마인가?'에 대한 답을 찾기 위함이다. 이는 다음의 식으로 나타낼 수 있다.
$$
P(A|B) = \frac{P(A\cap B)}{P(B)} \\
P(B)P(A|B) = P(A\cap B)
$$
그리고 'A가 일어났을 때 B가 일어날 확률' 또한 다음과 같이 표현할 수 있다.
$$
P(B|A) = \frac{P(B\cap A)}{P(A)} \\
P(A)P(B|A) = P(B\cap A)
$$
여기서 $P(A\cap B) = P(B \cap A)$이므로 이를 풀어 쓰면 다음과 같다.
$$
P(A|B) = \frac{P(B|A)P(A)}{P(B)}
$$
$P(B)$는 다음과 같이 표현할 수 있다.
$$
P(B) = \sum_{a \in A} P(B \cap A) = \sum_{a \in A} P(B|A)P(A)
$$
즉, 교집합에 대한 확률을 모든 A의 이벤트에 대해 더해준 값이다. 그러므로 마지막으로 조건부 확률을 다음과 같이 쓸 수 있다.
$$
P(A|B) = \frac{P(B|A)P(A)}{ \sum_{a \in A} P(B|A)P(A)}
$$
우리가 동전 던지기에서 알고싶은 것은 '동전이 얼마나 공정(fair)한가?'이다. 즉, 동전의 앞면이 나올 확률이 정말 거의 0.5에 가까운가를 알고싶은 것이다. Bayes 추론을 이 문제에 적용하기위해 다음과 같은 과정을 따라야 한다.
1) Assumptions - 동전은 무조건 두 결과(앞, 뒤) 중 하나만 나온다고 가정한다. 물론 동선을 던졌을 때 서 있을 수 있지만, 이런 상황은 제외한다. 그리고 각 시도에서 나오는 결과는 다른 시도에서 나오는 결과와 독립적이며, 이 공정성(fairness)는 어느 시도에서건 안정적(stationary)이므로 시간에 따라 달라지거나 하지 않는다. 여기서 공정성은 $\theta$라는 인수로 표현하자.
2) Prior Beliefs - 추론을 적용하기 위해 이 prior beliefs(선행 믿음?)을 정량화해야 한다. 이는 우리가 찾아볼 공정성의 분포를 특정하는 것으로 귀결된다.
3) Experimental Data - 이제 동전을 던져 실제 데이터를 뽑아낸다. 이 때 어떤 $\theta$가 주어졌을 때 해당 실제 결과가 나올 확률이 필요한데, 이 것이 likelihood function이다.
4) Posterior Beliefs - 이제 앞의 Bayes' rule을 이용하여 데이터에 기반한 새로운 확률을 구한다. 앞서 prior beliefs 과정에서 Beta distribution와 Bernoulli likelihood function을 사용하면 posterior에서도 beta distribution을 얻을 수 있는데, 이렇게 posterior와 prior가 같은 형태의 분포로 표현되는 것을 conjugate priors라고 한다.
5) Inference - 구해진 posterior belief를 기반으로 동전의 공정성을 추정한다.
앞서의 Bayes' Rule로 표현한 다음 식과 위의 과정을 대입해보면 다음과 같다.
$$
P(\theta | D) = P(D|\theta)P(\theta) / P(D)
$$
여기서 D는 data이다.
확률 변수 $k$가 동전 던지기의 결과를 나타낸다고 하면 $k \in \{ 0, 1 \}$이다. 여기서 앞면이 나올 확률(공정성)을 $\theta$라 했으니, $\theta$가 주어졌을 때 $k$의 확률을 다음과 같이 쓸 수 있다.
$$
P(k|\theta) = \theta^{k}(1-\theta)^{1-k}
$$
위의 식을 다시 해석하면 특정 $\theta$가 주어졌을 때 $k$의 확률을 나타내므로 결국 likelihood function으로 해석할 수 있다.
이제 동전을 여러번 던진다고 하자. 각각의 던지는 행동은 독립적이므로 각각의 확률을 곱하면 총 확률을 구할 수 있다. 즉, 다음과 같은 식으로 쓸 수 있다.
$$
P(\{k_1, \ldots , K_N\}|\theta) = \prod_{i} P(k_i | \theta) = \prod_{i} \theta^{k_i}(1-\theta)^{1-k_i}
$$
N번 던졌을 때 z번의 앞면이 나왔다면 위의 식은 다음과 같이 쓸 수 있다.
$$
P(z, N|\theta)=\theta^{z} (1-\theta)^{N-z}
$$
앞서 얘기했듯이 $\theta$에 대한 분포를 일단 정해야 한다. 여기서 $\theta \in [0, 1]$이니 beta distribution을 사용한다. beta distribution의 PDF(확률밀도함수)는 다음과 같다.
$$
P(\theta | \alpha, \beta) = \theta^{\alpha - 1} ( 1- \theta)^{\beta - 1} / B(\alpha, \beta)
$$
여기서 $B(\alpha, \beta)$는 값을 0과 1사이에 위치시키기 위한 표준화 상수(normalization constant)로서 다음과 같이 쓴다.
$$
B(\alpha, \beta) = \frac{\Gamma (\alpha)\Gamma (\beta)}{\Gamma (\alpha + \beta)} = \frac{(\alpha - 1)!(\beta - 1)!}{(\alpha + \beta - 1)!}
$$
위 분포의 $\alpha$와 $\beta$에 따른 모습은 다음 그림과 같다.
Beta prior(beta distribution으로 표현한 prior)의 $\alpha , \beta$를 이용하여 조금 더 친숙한 mean, variance를 표현할 수 있다. 이는 다음과 같다.
$$
\mu = \frac{\alpha}{\alpha + \beta}, \\
\sigma = \sqrt{\frac{\alpha \beta}{(\alpha + \beta)^2(\alpha + \beta + 1)}}
$$
Bayes' rule을 이용하여 posterior를 바꿔보자. 일단 위의 likelihood 함수 등을 이용하면 다음과 같이 표현할 수 있다.
$$
\begin{eqnarray}
P(\theta | z, N) &=& P(z, N|\theta)P(\theta) / P(z, N) \\
&=& \theta^{z} (1-\theta)^{N-z} \theta^{\alpha - 1}(1-\theta)^{\beta - 1} / [B(\alpha, \beta)P(z, N)] \\
&=& \theta^{z+\alpha - 1}(1-\theta)^{N-z+\beta - 1} / B(z+\alpha, N-z+\beta)
\end{eqnarray}
$$
실제 coding을 해서 그 distribution을 그려보면 다음과 같이 횟수가 늘어날 수록 $\theta$가 0.5 근처로 몰리는 것을 볼 수 있다.
1. Bayesian vs. Frequentist
통계 문제에 확률을 적용하는 방법은 크게 'Bayesian'과 'Frequentist'가 있다. 'Frequentist'는 확률이란 어느 사건이 아주 많은 수의 수행 속에 나타난 빈도라고 생각하는 것이다. 그래서 이 경우 ideal 확률을 알아야 하며, 이 값이 변하지 않는다.
'Bayesian'의 경우, 이미 일어난 사건(data)와 앞으로 일어날 사건을 바탕으로 우리가 믿고있는 확률을 변화시킬 수 있다고 한다.
최근 이슈가되는 Machine Learning이나, 예전부터 많이 사용되는 Time Series Analysis는 모두 Bayesian Statistics에 바탕을두고있다.
2. Bayes' Rule
Bayes' Rule은 조건부 확률(conditional probability), 즉, 'B라는 일이 일어났을 때 A라는 일이 일어날 확률은 얼마인가?'에 대한 답을 찾기 위함이다. 이는 다음의 식으로 나타낼 수 있다.
$$
P(A|B) = \frac{P(A\cap B)}{P(B)} \\
P(B)P(A|B) = P(A\cap B)
$$
그리고 'A가 일어났을 때 B가 일어날 확률' 또한 다음과 같이 표현할 수 있다.
$$
P(B|A) = \frac{P(B\cap A)}{P(A)} \\
P(A)P(B|A) = P(B\cap A)
$$
여기서 $P(A\cap B) = P(B \cap A)$이므로 이를 풀어 쓰면 다음과 같다.
$$
P(A|B) = \frac{P(B|A)P(A)}{P(B)}
$$
$P(B)$는 다음과 같이 표현할 수 있다.
$$
P(B) = \sum_{a \in A} P(B \cap A) = \sum_{a \in A} P(B|A)P(A)
$$
즉, 교집합에 대한 확률을 모든 A의 이벤트에 대해 더해준 값이다. 그러므로 마지막으로 조건부 확률을 다음과 같이 쓸 수 있다.
$$
P(A|B) = \frac{P(B|A)P(A)}{ \sum_{a \in A} P(B|A)P(A)}
$$
3. Coin flipping에 Bayes 추론 적용하기
우리가 동전 던지기에서 알고싶은 것은 '동전이 얼마나 공정(fair)한가?'이다. 즉, 동전의 앞면이 나올 확률이 정말 거의 0.5에 가까운가를 알고싶은 것이다. Bayes 추론을 이 문제에 적용하기위해 다음과 같은 과정을 따라야 한다.
1) Assumptions - 동전은 무조건 두 결과(앞, 뒤) 중 하나만 나온다고 가정한다. 물론 동선을 던졌을 때 서 있을 수 있지만, 이런 상황은 제외한다. 그리고 각 시도에서 나오는 결과는 다른 시도에서 나오는 결과와 독립적이며, 이 공정성(fairness)는 어느 시도에서건 안정적(stationary)이므로 시간에 따라 달라지거나 하지 않는다. 여기서 공정성은 $\theta$라는 인수로 표현하자.
2) Prior Beliefs - 추론을 적용하기 위해 이 prior beliefs(선행 믿음?)을 정량화해야 한다. 이는 우리가 찾아볼 공정성의 분포를 특정하는 것으로 귀결된다.
3) Experimental Data - 이제 동전을 던져 실제 데이터를 뽑아낸다. 이 때 어떤 $\theta$가 주어졌을 때 해당 실제 결과가 나올 확률이 필요한데, 이 것이 likelihood function이다.
4) Posterior Beliefs - 이제 앞의 Bayes' rule을 이용하여 데이터에 기반한 새로운 확률을 구한다. 앞서 prior beliefs 과정에서 Beta distribution와 Bernoulli likelihood function을 사용하면 posterior에서도 beta distribution을 얻을 수 있는데, 이렇게 posterior와 prior가 같은 형태의 분포로 표현되는 것을 conjugate priors라고 한다.
5) Inference - 구해진 posterior belief를 기반으로 동전의 공정성을 추정한다.
앞서의 Bayes' Rule로 표현한 다음 식과 위의 과정을 대입해보면 다음과 같다.
$$
P(\theta | D) = P(D|\theta)P(\theta) / P(D)
$$
여기서 D는 data이다.
- $P(\theta)$ - prior. 여기서 data D에 대한 감안은 없다.
- $P(\theta | D)$ - posterior. 수정된 우리의 믿음이라고 보면 된다.
- $P(D| \theta)$ - likelihood. 어떤 인수 $\theta$가 있을 때 관찰한 데이터가 나올 확률이다.
- $P(D)$ - evidence. 모든 $\theta$에 대해 D가 나올 확률을 더한 확률
3.1 Bernoulli Distribution의 Likelihood Function
확률 변수 $k$가 동전 던지기의 결과를 나타낸다고 하면 $k \in \{ 0, 1 \}$이다. 여기서 앞면이 나올 확률(공정성)을 $\theta$라 했으니, $\theta$가 주어졌을 때 $k$의 확률을 다음과 같이 쓸 수 있다.
$$
P(k|\theta) = \theta^{k}(1-\theta)^{1-k}
$$
위의 식을 다시 해석하면 특정 $\theta$가 주어졌을 때 $k$의 확률을 나타내므로 결국 likelihood function으로 해석할 수 있다.
이제 동전을 여러번 던진다고 하자. 각각의 던지는 행동은 독립적이므로 각각의 확률을 곱하면 총 확률을 구할 수 있다. 즉, 다음과 같은 식으로 쓸 수 있다.
$$
P(\{k_1, \ldots , K_N\}|\theta) = \prod_{i} P(k_i | \theta) = \prod_{i} \theta^{k_i}(1-\theta)^{1-k_i}
$$
N번 던졌을 때 z번의 앞면이 나왔다면 위의 식은 다음과 같이 쓸 수 있다.
$$
P(z, N|\theta)=\theta^{z} (1-\theta)^{N-z}
$$
3.2 Prior Beliefs의 정량화
앞서 얘기했듯이 $\theta$에 대한 분포를 일단 정해야 한다. 여기서 $\theta \in [0, 1]$이니 beta distribution을 사용한다. beta distribution의 PDF(확률밀도함수)는 다음과 같다.
$$
P(\theta | \alpha, \beta) = \theta^{\alpha - 1} ( 1- \theta)^{\beta - 1} / B(\alpha, \beta)
$$
여기서 $B(\alpha, \beta)$는 값을 0과 1사이에 위치시키기 위한 표준화 상수(normalization constant)로서 다음과 같이 쓴다.
$$
B(\alpha, \beta) = \frac{\Gamma (\alpha)\Gamma (\beta)}{\Gamma (\alpha + \beta)} = \frac{(\alpha - 1)!(\beta - 1)!}{(\alpha + \beta - 1)!}
$$
위 분포의 $\alpha$와 $\beta$에 따른 모습은 다음 그림과 같다.
Beta prior(beta distribution으로 표현한 prior)의 $\alpha , \beta$를 이용하여 조금 더 친숙한 mean, variance를 표현할 수 있다. 이는 다음과 같다.
$$
\mu = \frac{\alpha}{\alpha + \beta}, \\
\sigma = \sqrt{\frac{\alpha \beta}{(\alpha + \beta)^2(\alpha + \beta + 1)}}
$$
3.3 Posterior 계산하기
Bayes' rule을 이용하여 posterior를 바꿔보자. 일단 위의 likelihood 함수 등을 이용하면 다음과 같이 표현할 수 있다.
$$
\begin{eqnarray}
P(\theta | z, N) &=& P(z, N|\theta)P(\theta) / P(z, N) \\
&=& \theta^{z} (1-\theta)^{N-z} \theta^{\alpha - 1}(1-\theta)^{\beta - 1} / [B(\alpha, \beta)P(z, N)] \\
&=& \theta^{z+\alpha - 1}(1-\theta)^{N-z+\beta - 1} / B(z+\alpha, N-z+\beta)
\end{eqnarray}
$$
실제 coding을 해서 그 distribution을 그려보면 다음과 같이 횟수가 늘어날 수록 $\theta$가 0.5 근처로 몰리는 것을 볼 수 있다.
북유럽 신화(닐 게이먼, 2017)
0. 마블 코믹스의 영화가 세계적으로 히트를하면서 '어벤저스' 등에 나온 '토르', '로키'는 이제 매우 유명한 캐릭터가 되었다. 그리고 판타지 소설의 고전이라 불리는 '반지의 제왕'이 있고, 최근에는 '왕좌의 게임'이 있다. 이 두 판타지 소설들은 그 설정이 많은 부분 북유럽 신화에 나오는 내용에 바탕을 두고 있고, '토르'와 '로키'는 아예 북유럽 신화의 주인공들이다.
1. 시초의 거인 이미르에서 시작하여 오딘, 그의 아들 토르와 거인족 라우페이의 아들 로키가 겪는 일들이 북유럽 신화 이야기의 큰 축을 이룬다. 그리고 마지막장의 라그나로크에서 신들의 마지막 싸움과 멸망을 그린다.
북유럽신화는 그리스 신화와 다르게 상당히 내용이 거칠고 어둡다. 저술 과정에서 아마도 순화되었겠으나, 꽤나 잔혹한 장면이 많고, 별 것아닌 동기로 잔혹하게 상대방을 살해하는 듯한 내용도 꽤 많다. 아마도 이것은 이야기가 전승되어오는 북유럽의 고대 바이킹들의 성정이 반영된 것이 아닌가 한다. 전승되어오는 국가 또는 장소의 역사와 신화의 분위기를 엮어본다면 꽤 재미있는 주제가 될 듯하다. 실제 그리스 신화의 신들은 매우 부유하고 사치스럽다.
2. 닐게이먼은 알고보니 꽤나 유명한 작가였다. 그래픽노블 작가이고, 그 외 소설로 상도 많이 탔다. 덕분에 책의 내용들이 술술 읽히며 이야기가 매우 흥미롭다. 번역도 나름 괜찮은 편이어서 읽는데 부데끼지 않는다. 기분 전환하기 참 좋은 책인 듯 싶다.
1. 시초의 거인 이미르에서 시작하여 오딘, 그의 아들 토르와 거인족 라우페이의 아들 로키가 겪는 일들이 북유럽 신화 이야기의 큰 축을 이룬다. 그리고 마지막장의 라그나로크에서 신들의 마지막 싸움과 멸망을 그린다.
북유럽신화는 그리스 신화와 다르게 상당히 내용이 거칠고 어둡다. 저술 과정에서 아마도 순화되었겠으나, 꽤나 잔혹한 장면이 많고, 별 것아닌 동기로 잔혹하게 상대방을 살해하는 듯한 내용도 꽤 많다. 아마도 이것은 이야기가 전승되어오는 북유럽의 고대 바이킹들의 성정이 반영된 것이 아닌가 한다. 전승되어오는 국가 또는 장소의 역사와 신화의 분위기를 엮어본다면 꽤 재미있는 주제가 될 듯하다. 실제 그리스 신화의 신들은 매우 부유하고 사치스럽다.
2. 닐게이먼은 알고보니 꽤나 유명한 작가였다. 그래픽노블 작가이고, 그 외 소설로 상도 많이 탔다. 덕분에 책의 내용들이 술술 읽히며 이야기가 매우 흥미롭다. 번역도 나름 괜찮은 편이어서 읽는데 부데끼지 않는다. 기분 전환하기 참 좋은 책인 듯 싶다.
잡설 3 - 오늘의 운세
2003년이었던 것 같다. 대학원 진학 후 좋지 않은 일들이 있었고, 대인관계가 힘들어 하루하루가 고통이었다. 답도 잘 안나오고 하니 인터넷으로 운세도 찾아보고 그랬다. 그러다 전화로 하는 유료 운세상담을 5천원 주고 해보기도 했었다. 그 때 말로는 6월인가 지나면 나아질 것이라고 했는데, 사실 별 일이 일어나지도 않았고 그냥 그런 날들이 계속되고 있었다.
2014년도 비슷했다. 처음 트레이딩이라는 것을 시작하고 잘못된 모형으로 손실을 입었을 때, 여기저기서 들어오는 압박이 너무 힘들기도 했고, 처음 겪는 일에 괴로움의 강도가 너무 강했었다. 그 때도 여기저기 오늘의 운세나 보며 무언가 돌파구가 생기길 바랬었다. 하지만 역시나 맞는 것은 별로 없었고, 그저 시간이 지나면서 어떻게 어떻게 흘러갔다.
그런 일들을 겪으며 그나마 배운 것은 그래도 시간이 지나면, 물론 허투루 시간을 보내지 않는다는 기본 가정을 지킨다면, 일이 어떻게든 해결은 난다는 것이었다. 그 것이 유야무야 되어 잊혀지든, 아니면 해결 방안이 생기든 말이다.
요즘 내 모습을 보면 저 때와 비교해 그다지 나아진 것 같지는 않다. 시간이 지나더라도 어떤 일들이 고통스러운 것은 그대로이고, 그 때마다 마음이 급해져 요행을 바라는 것도 말이다. 요즘도 혹시나 하는 기대로 오늘의 운세를 뒤적거리기도 한다. 지금처럼 삶을 잘 유지하며 버티면 다 끝이 보이겠지만, 그럼에도 마음이 급해지는 이유는 무엇일까?
2014년도 비슷했다. 처음 트레이딩이라는 것을 시작하고 잘못된 모형으로 손실을 입었을 때, 여기저기서 들어오는 압박이 너무 힘들기도 했고, 처음 겪는 일에 괴로움의 강도가 너무 강했었다. 그 때도 여기저기 오늘의 운세나 보며 무언가 돌파구가 생기길 바랬었다. 하지만 역시나 맞는 것은 별로 없었고, 그저 시간이 지나면서 어떻게 어떻게 흘러갔다.
그런 일들을 겪으며 그나마 배운 것은 그래도 시간이 지나면, 물론 허투루 시간을 보내지 않는다는 기본 가정을 지킨다면, 일이 어떻게든 해결은 난다는 것이었다. 그 것이 유야무야 되어 잊혀지든, 아니면 해결 방안이 생기든 말이다.
요즘 내 모습을 보면 저 때와 비교해 그다지 나아진 것 같지는 않다. 시간이 지나더라도 어떤 일들이 고통스러운 것은 그대로이고, 그 때마다 마음이 급해져 요행을 바라는 것도 말이다. 요즘도 혹시나 하는 기대로 오늘의 운세를 뒤적거리기도 한다. 지금처럼 삶을 잘 유지하며 버티면 다 끝이 보이겠지만, 그럼에도 마음이 급해지는 이유는 무엇일까?
옥자(2017, 봉준호)
0. 무려 500억 가량의 제작비를 들여 만든 넷플릭스 오리지널 무비다. 스토리 설명이야 워낙 많은 곳에서 하고있으니, 간단히 소감만 적어보려한다.
1. 옥자에서 좋았던 점은, 일단 그래픽과 옥자 캐릭터가 좋다. 서글서글한 눈매에 하마인 듯하고, 다시 보면 매너티 같기도 한 이 슈퍼돼지는, 표정만 봐도 편안하고 기분이 좋아진다. 거기에 안서현양이 분한 미자와 함께 꽁냥거리는 장면은 흐뭇하게 바라볼 수 있다.
그리고 이 영화의 메시지가 좋다. 개인적으로 채식주의자도 아니고 가히 고기테리안에 가까운 나지만, 한 번쯤 대량생산 품목처럼 취급되는 동물들에 대해 생각해볼만한 기회를 준다. 결론 자체도 의외인데, 한 마디로 설명하자면, 판타지같은 영화에 너무나도 현실적인 결말이다. 물론 이 결말때문에 호불호가 갈리는 듯한 인상이 있다.
마지막으로 배우들의 연기가 좋다. 어느 하나 발연기가 없어 마음에 들었다.
2. 그런데, 이 영화가 몇가지 애매한 점이 있다. 일단 캐릭터들이 색이 조금 불 분명하다. 전작 '괴물', '마더' 등에서는 캐릭터가 꽤나 색이 강하고, 그럼에도 영화속에서 각과 부드러움을 적절히 버무렸는데, '옥자'에선 그런 것들이 조금 약했다. 그리고 결말이 어떤 영화적 카타르시스를 기대하기는 무리이다보니, 호불호가 갈릴 수밖에 없다. 하지만 영화 자체의 내용을 놓고보면 결말로 가는 과정이 어거지거나, 난삽하거나하진 않아 보인다. 개인적으로 결말로만 보면 '마더'가 압권이었다. 그 뽕 맞은 듯한 엔딩은...
3. 봉감독의 헐리웃 데뷔작인 '설국열차'는 처음엔 뭔가 무거웠지만, 그래도 두 세번 보더라도 재미가 반감되는 느낌은 없었다. 그래서 국내에선 호불호가 갈렸지만, '설국열차'를 꽤 좋아한다. 이번 '옥자'는 어떨지 모르겠다. '설국열차'에 비하면 힘이 많이 빠졌지만, 메시지는 더욱 직접적이다. 캐릭터는 조금 약해도 헐리웃 배우들의 명연기를 보는 맛은 있다. 결론적으로, 나는 재미있게 잘 봤다.
Uncopyable class와 clone 함수
C++의 경우 class를 생성하면 기본적으로 default constructor와 copy constructor, 대입 연산자가 기본으로 만들어진다. 이 세가지는 프로그래머가 작성하지 않더라도 컴파일러가 알아서 마치 사람이라면 밥 먹고 화장실 가듯이 자연스럽게 만들어 버린다.
C++의 가장 어려운 점이자, OOP(Object Oriented Programming)이라면 어느 언어든 가지고 있는 문제는 객채의 state 관리이다. Class도 하나의 type으로 보므로 각종 사칙 연산의 overloading이 가능한데다, 구조 안에 다양한 class의 객체를 state variable로 가질 수 있어 까딱 잘못하단 지옥문이 열린다. 특히 멀티 쓰레드 환경에선 더 심하다.(덕분에 Functional Programming 추종자들에게 대차게 까이지만, FP도 VM은 C++로 만든게 많다. -_-)
이런 고통을 조금이나마 완화할 수 있는 방법은, class 자체의 복사를 막아버리는 것이다. 물론 다 막으라는 것이 아니라, 한 클래스의 각각의 객체가 서로 독립적인 상태를 가져야 한다든가, copy는 허용하고 싶은데 내용물에 pointer가 있다던가 하는 경우에 고려할만하다. 특히 후자의 pointer를 내용물로 가졌을 때는 앞에 소개할 방법을 심각하게 고려해봐야 한다.
다음과 같은 코드를 실행해보자.
이 코드를 실행하면 다음과 같은 결과를 얻을 수 있다.
즉, 같은 위치의 메모리 영역을 가리키게 되고, 한 객체에서 메모리 영역 내의 값을 바꾸면 다른 객채까지 영향을 준다.
이런 문제를 해결하기 위해서는 일단 class의 기본적인 복사를 막는다. 다음과 같이 Uncopyable이라는 클래스를 선언하고 copy constructor와 대입연산자를 private으로 선언한다.
그리고 다음 처럼 위의 클래스를 상속한 클래스를 만들어주자.
위의 코드를 컴파일하면 Uncopyable 클래스에 대한 access violation이 일어나면서 컴파일이 되지 않는다. 그리고 베이스 클래스에 가상 함수로 clone이라는 것을 지정하여 하위 클래스가 clone을 구현하도록 하면 내가 원하는 방식으로 객체 복사를 할 수 있다.
개인적으로도 이 방식을 잘 활용하는데, 아직까지는 꽤 성공적인 듯 하다.
C++의 가장 어려운 점이자, OOP(Object Oriented Programming)이라면 어느 언어든 가지고 있는 문제는 객채의 state 관리이다. Class도 하나의 type으로 보므로 각종 사칙 연산의 overloading이 가능한데다, 구조 안에 다양한 class의 객체를 state variable로 가질 수 있어 까딱 잘못하단 지옥문이 열린다. 특히 멀티 쓰레드 환경에선 더 심하다.(덕분에 Functional Programming 추종자들에게 대차게 까이지만, FP도 VM은 C++로 만든게 많다. -_-)
이런 고통을 조금이나마 완화할 수 있는 방법은, class 자체의 복사를 막아버리는 것이다. 물론 다 막으라는 것이 아니라, 한 클래스의 각각의 객체가 서로 독립적인 상태를 가져야 한다든가, copy는 허용하고 싶은데 내용물에 pointer가 있다던가 하는 경우에 고려할만하다. 특히 후자의 pointer를 내용물로 가졌을 때는 앞에 소개할 방법을 심각하게 고려해봐야 한다.
다음과 같은 코드를 실행해보자.
class B
{
public:
B(int i)
{
k = new int;
(*k) = i;
}
int val()
{
return *k;
}
int* valp()
{
return k;
}
private:
int *k;
};
...
B b(1);
B b3 = b;
std::cout << "b : " << b.valp() << std::endl;
std::cout << "b3 : " << b3.valp() << std::endl;
이 코드를 실행하면 다음과 같은 결과를 얻을 수 있다.
b : 0047AD50
b3 : 0047AD50
즉, 같은 위치의 메모리 영역을 가리키게 되고, 한 객체에서 메모리 영역 내의 값을 바꾸면 다른 객채까지 영향을 준다.
이런 문제를 해결하기 위해서는 일단 class의 기본적인 복사를 막는다. 다음과 같이 Uncopyable이라는 클래스를 선언하고 copy constructor와 대입연산자를 private으로 선언한다.
class Uncopyable
{
public:
Uncopyable() {}
~Uncopyable() {}
private:
Uncopyable(const Uncopyable&);
Uncopyable& operator=(const Uncopyable&);
};
그리고 다음 처럼 위의 클래스를 상속한 클래스를 만들어주자.
class A : private Uncopyable
{
public:
A(int i)
{
k = i;
}
int val()
{
return k;
}
private:
int k;
};
A a(1);
A a2 = a;
위의 코드를 컴파일하면 Uncopyable 클래스에 대한 access violation이 일어나면서 컴파일이 되지 않는다. 그리고 베이스 클래스에 가상 함수로 clone이라는 것을 지정하여 하위 클래스가 clone을 구현하도록 하면 내가 원하는 방식으로 객체 복사를 할 수 있다.
class Base
{
public:
...
virtual Base* clone() = 0;
}
개인적으로도 이 방식을 잘 활용하는데, 아직까지는 꽤 성공적인 듯 하다.
잡설 2 - 고개 숙임
90년대 월드와이드웹이 개발되어 퍼지고, 네트워크를 컴퓨터에 연결하면서 사람들은 새로운 세상을 경험했다. 어디서든 컴퓨터가 있는 곳이라면 누구나 정보를 열람할 수 있고, 각종 채팅 서비스들로 일면식도 없는 사람과 대화를 나누었다. 그리고 그와 함께 사람들이 모이는 커뮤니티라는 것이 생기고, 그 안에서 각자의 모습을 분출하며, 누군가는 그 안에서 스타가 되기도 하였다.
2008년 경 아이폰의 출시는 이런 인터넷 사용 모습을 완전히 바꾸어놓았다. 물론 아이폰 이전에도 인터넷이 되는 전화기는 이미 많이 있었고, 스마트폰이라는 개념도 사실 없던 것이 아니었다. 하지만 누구나 앱(app)을 개발할 수 있고, 다양한 기능을 앱을 통해 사용할 수 있다는 개념을 대중화시킨 것은 분명 아이폰이다.
이렇게 손으로 들고다닐 수 있는 전화기는 통신망을 통해 언제 어디서나 인터넷에 접속할 수 있었고, 이를 바탕으로 다양한 서비스가 폭발적으로 성장했다. 그러다보니 사람들은 언제 어디서나 다른 사람들의 소식을 들을 수 있었고, 자신의 소식과 생각을 공유할 수 있었다.
출퇴근 시간에 전철이나 버스에서 고성능 스마트폰으로 여러 소식에 심취해있는 모습은 이미 오래된 풍경이다. 그리고 길을 가다 무슨 일이 생기면 그 것을 공유하기 위해 스마트폰을 들이대는 모습도 현 시대 인류의 스테레오타입이 돼버린지 오래다. 물론 나도 예외는 아니리라.
이런 고개 숙인 인간상은 비단 교통수단 안에서 혼자 있을 때만 한정되진 않는 것 같다. 식당이나 공원, 또는 여러 곳에서 여러 사람이 모여있더라도 서로 이야기를 나누기 보단 고개를 숙이고 스마트폰을 본다. 분명 만나고 싶어서 만난 사람들일텐데, 옆에 있는 사람보다 더 멀리있는 누군가의 소식이 더 궁금한가보다.
그리고 길을 가다보면 무엇이 그리 궁금한지 스마트폰에 눈을 고정하고 위태위태하게 걷는 사람들도 많이 있다. 물론 그들의 사정이 있겠지만, 길을 가는 사람들을 너무 방해하는 것이 아닌가 하는 생각도 든다.
어디서나 시간과 공간에 구애받지 않고 소식을 얻을 수 있는 자유는 얻었다. 하지만 그 것이 과연 진정한 연결을 제공하는지는 다시 생각해볼 문제인 것 같다.
2008년 경 아이폰의 출시는 이런 인터넷 사용 모습을 완전히 바꾸어놓았다. 물론 아이폰 이전에도 인터넷이 되는 전화기는 이미 많이 있었고, 스마트폰이라는 개념도 사실 없던 것이 아니었다. 하지만 누구나 앱(app)을 개발할 수 있고, 다양한 기능을 앱을 통해 사용할 수 있다는 개념을 대중화시킨 것은 분명 아이폰이다.
이렇게 손으로 들고다닐 수 있는 전화기는 통신망을 통해 언제 어디서나 인터넷에 접속할 수 있었고, 이를 바탕으로 다양한 서비스가 폭발적으로 성장했다. 그러다보니 사람들은 언제 어디서나 다른 사람들의 소식을 들을 수 있었고, 자신의 소식과 생각을 공유할 수 있었다.
출퇴근 시간에 전철이나 버스에서 고성능 스마트폰으로 여러 소식에 심취해있는 모습은 이미 오래된 풍경이다. 그리고 길을 가다 무슨 일이 생기면 그 것을 공유하기 위해 스마트폰을 들이대는 모습도 현 시대 인류의 스테레오타입이 돼버린지 오래다. 물론 나도 예외는 아니리라.
이런 고개 숙인 인간상은 비단 교통수단 안에서 혼자 있을 때만 한정되진 않는 것 같다. 식당이나 공원, 또는 여러 곳에서 여러 사람이 모여있더라도 서로 이야기를 나누기 보단 고개를 숙이고 스마트폰을 본다. 분명 만나고 싶어서 만난 사람들일텐데, 옆에 있는 사람보다 더 멀리있는 누군가의 소식이 더 궁금한가보다.
그리고 길을 가다보면 무엇이 그리 궁금한지 스마트폰에 눈을 고정하고 위태위태하게 걷는 사람들도 많이 있다. 물론 그들의 사정이 있겠지만, 길을 가는 사람들을 너무 방해하는 것이 아닌가 하는 생각도 든다.
어디서나 시간과 공간에 구애받지 않고 소식을 얻을 수 있는 자유는 얻었다. 하지만 그 것이 과연 진정한 연결을 제공하는지는 다시 생각해볼 문제인 것 같다.
잡설 1
지금 사는 행신에서 직장이 있는 을지로까지 출퇴근 하는데, 대략 한시간이 덜 걸린다. 행신역에서 전철을 타고 갈 수 있고, 집 앞 버스 정류소에서 버스를 타고 신촌으로 나올 수도 있다. 전철을 타면 신촌/홍대입구까지 전철 타는 시간만 20분 남짓이면 되지만, 버스는 막히면 40분을 넘기기 일쑤다.
그럼에도 종종 버스를 타고 출근을 하는 이유는 나름 상반된 풍경을 즐길 수 있어서다.
베드타운 성격이 강할지언정 나름 도시의 모습을 잘 갖춘 행신을 빠져나오면 쭉 뻗은 도로 양 옆으로 간판이 바랜 상점들이 꽤 즐비하게 서있다. 하지만, 그 뒤로는 멀리 북한산이 보이고, 넓은 초지가 펼쳐져있어 마치 한적한 시골에 와 있는 느낌이 든다. 그렇게 한 15분여를 달리면 서울의 경계에 있는 수색에 다다른다.
수색과 가좌는 2010년도 넘어서나 재개발이 이루어진 곳이라 참 묘한 풍경을 하고 있다. 도로가에는 딱 봐도 정말 오래된 상점들과 상가들이 있지만, 바로 뒤 블럭을 보거나 조금만 그 곳을 지나가면 새로지은 거대한 아파트 단지가 눈에 들어온다. 또 눈을 오른쪽으로 돌리면 '디지털미디어시티'라는 거창한 이름을 가진 거대한 상업/업무지구가 눈에 들어온다.
이곳을 지날때마다 과연 이런 개발이 이루어지기 전 이곳의 모습이 어땠을지 궁금해진다. 길가를 따라 들쭉날쭉 지어진 허름한 건물들이 주는 풍경과, 무 자른 듯 딱 떨어지는 각도로 서있는 아파트의 풍경이 너무나도 대조적이기 때문이다.
아마도 예전엔 그저 사람들이 소소히 모여사는 작은 마을이었겠지. 아니면 이전에도 이미 사람들이 몰려사는 시끄러운 동네였을까. 누군가는 재개발의 수혜를 입었을테고, 누군가는 삶의 터전을 빼앗겼겠지. 이런저런 생각이 든다.
그리고 이런 대조적 풍경도 지나고 거대도시 속으로 버스는 쑥 빨려들어간다. 대충 시간을 계산해보면 늦지는 않겠구나 안도하며 지하철로 갈아타고 나는 인파속으로 총총히 사라진다.
완벽한 공부법 (2017, 고영성, 신영준)

0. 이 책은 2017년 초반 발행되어 베스트셀러에 등극하며 나름 센세이션을 일으켰다.
1. 이런 류의 자기 계발 서적은 어떤 것은 너무 자기 위주의 내용을 진리인양 써서 거부감을 일으키기도 하고 현실과 어울리지 않는 경우도 많이 있다. 이 책은 조금 다른 것이 저자들이 이것 저것 열심히 찾아보고, 공부하고, 짜집고 쓴 책이기 때문에 꽤나 도움되는 내용이 많다. 거기에 저자들의 경험이 녹아들어 한 번쯤은 읽어보는 것이 도움될 듯 하다.
2. 완벽한 공부법의 내용을 요약하면 다음과 같은 키워드로 정리할 수 있다. 기억을 더듬기 위해 가끔 들춰보면 앞으로도 도움이 많이 될 듯하다.
- 자기 자신을 믿고 작은 성공부터
- 자기 자신을 아는 메타인지
- 기억 잘하기(공부는 어렵게)
- 시험효과
- 인출효과(시험,안성,토론,요약,글쓰기,발표 등)
- 분산연습 - 몰아치는 것이 아닌 시기를 나눠서
- 교차 - 두 가지 이상을 번갈아가며
- 그 외 - 자기참조, 맥락, 심상활용, 조직화, 첫 낱자 조합
- 감정
- 부정적 감정보다 긍정적 감정이 학습효과를 높임
- 부정적이거나 걱정되는 감정을 표현하거나 긍정적 감정으로 바꿔주면 효율이 높아짐
- 사회성
- 외로운 사람은 학습 능력 저하
- 사람과의 관계를 잘 유지해야 함
- 환경
- 습관은 의지력이 아닌 알람으로 고침
- 스스로 집중이 잘 되는 환경 필요
- 스마트폰 쉣
- 창의성
- 있던 아이디어들의 새로운 조합
- 그래서 다양한 경험 필요(취미, 여행, 독서 등)
- 독서
- 다양한 경험 필요
- 독서를 많이 해라
- 다독 후 정독으로
로건(2017)
0. 만화로만 보던 'X-men'이 처음 실사 영화로 나왔을 때 그 충격은 이루 말할 수 없었다. 개인적으로 원작 팬이 아니었음에도 내용 자체에 빨려들어가서 푹 빠졌었다. 정말 양키스러운 원작의 코스츔을 입혀놓지 않아서 그런지 내용 몰입에 이질감이 없었다.
이 캐릭터 중 '울버린'을 맡은 '휴 잭맨'은 그가 아니면 울버린을 생각할 수 없을 정도로 엄청난 싱크로율을 보여주기도 했다.
1. 영화상의 설정이 아무리 늙지않는 뮤턴트이라 한들 사람이 늙지않을리 만무하다. 17년 전 휴 잭맨의 싱그러움은 세월 속으로 날아가고, 어느덧 얼굴에 깊게 패인 주름이 자리잡았다. 아무리 몸 관리를 한다고 해도 흐르는 세월을 속일 수는 없겠지. 확실히 울버린 스핀오프 시리즈를 보면 뒤로 갈수록 어쩔수 없이 느껴지는 세월의 흐름으로 아쉬움이 느껴지긴 했다. 상황이 이러면 영화를 제작하는 입장에서도 세대교체를 준비해야할 것이고, 특히 이 울버린이라는 정말 사랑받는 캐릭터의 경우는 그 고민이 더 깊었으리라 생각된다.
2. 마블 스튜디오는 로건의 퇴장을 비장하지만 오버하지 않는 이 <로건>이라는 영화를 통해 시도한다. 자연스럽게 새로운 울버린 X-23과 접점을 찾고, 구 배우들의 퇴장을 준비한다. 19금 히어로 무비라는 참 어색한 조합으로 영화가 나왔을 때 우려의 목소리가 있었으나, 오히려 작정한 듯한 액션이 이야기의 현실성을 더해준다. 여기에 세월에 찌든 로건의 자연스러운 욕지거리도 현실감에 한 몫한다.
3. 함께 하던 것과의 이별은 언제나 슬프다. 갓 성인이 되기 시작할 때부터 꼭 챙겨보던 X-men 시리즈의 한 세대가 그 끝을 고하는 모습을 보며 나 또한 그만큼 나이가 먹었음을 깨닫는다. 영화 자체의 건조하고 우울한 분위기도 한 몫하는 것 같다. 이렇게 멋지지만 슬픈 퇴장을 준비한 마블 스튜디오는 정말 장인정신이 있다는 생각도 들었다. 울버린, 프로페서 X, 그간 너무 행복했습니다.
X-men의 팬이라면, 아니 팬이 아니더라도 청소년 관람불가 히어로 무비가 궁금한 사람이라면 꼭 봐야할 영화.
이 캐릭터 중 '울버린'을 맡은 '휴 잭맨'은 그가 아니면 울버린을 생각할 수 없을 정도로 엄청난 싱크로율을 보여주기도 했다.
1. 영화상의 설정이 아무리 늙지않는 뮤턴트이라 한들 사람이 늙지않을리 만무하다. 17년 전 휴 잭맨의 싱그러움은 세월 속으로 날아가고, 어느덧 얼굴에 깊게 패인 주름이 자리잡았다. 아무리 몸 관리를 한다고 해도 흐르는 세월을 속일 수는 없겠지. 확실히 울버린 스핀오프 시리즈를 보면 뒤로 갈수록 어쩔수 없이 느껴지는 세월의 흐름으로 아쉬움이 느껴지긴 했다. 상황이 이러면 영화를 제작하는 입장에서도 세대교체를 준비해야할 것이고, 특히 이 울버린이라는 정말 사랑받는 캐릭터의 경우는 그 고민이 더 깊었으리라 생각된다.
2. 마블 스튜디오는 로건의 퇴장을 비장하지만 오버하지 않는 이 <로건>이라는 영화를 통해 시도한다. 자연스럽게 새로운 울버린 X-23과 접점을 찾고, 구 배우들의 퇴장을 준비한다. 19금 히어로 무비라는 참 어색한 조합으로 영화가 나왔을 때 우려의 목소리가 있었으나, 오히려 작정한 듯한 액션이 이야기의 현실성을 더해준다. 여기에 세월에 찌든 로건의 자연스러운 욕지거리도 현실감에 한 몫한다.
3. 함께 하던 것과의 이별은 언제나 슬프다. 갓 성인이 되기 시작할 때부터 꼭 챙겨보던 X-men 시리즈의 한 세대가 그 끝을 고하는 모습을 보며 나 또한 그만큼 나이가 먹었음을 깨닫는다. 영화 자체의 건조하고 우울한 분위기도 한 몫하는 것 같다. 이렇게 멋지지만 슬픈 퇴장을 준비한 마블 스튜디오는 정말 장인정신이 있다는 생각도 들었다. 울버린, 프로페서 X, 그간 너무 행복했습니다.
X-men의 팬이라면, 아니 팬이 아니더라도 청소년 관람불가 히어로 무비가 궁금한 사람이라면 꼭 봐야할 영화.
Machine Learning을 이용한 주가 패턴 분석(2) - Genetic Algorithm
0. 회사일 짬짬히 하다보니 아무래도 진도가 빠르진 않다. 하지만 하나 하나 해보며 정리를 하다보면 언젠간 결과가 나올 것이다.
일단 지난번에 Random Optimization을 가지고 테스트를 해봤다. 최적화라는 것이 어느정도 무작위성을 가지고 있는 것은 맞다. 아무래도 처음 답을 찍어서 이리저리 흔들어보며 더 나은 방향으로 나아가기 때문일 것이다. 하지만 너무 대놓고 무작위로 답을 찾아들어가면 작업을 많이 돌리면 돌릴수록 결과가 나아질 가능성이 높아지긴 하나 그 보장이 없으므로 무엇인가 안정적이면서 멋도 조금 나는 것들을 찾아보기로 했다.
최적화의 기본적인 알고리즘인 Hill Climb의 경우 이웃 해답이라는 개념이 있어야 하는데, 내가 풀고자 하는 문제에서는 이웃 해답을 정의하기가 애매했다. 그래서 멋도 나고 쓸만한 것으로 유전자 알고리즘을 선택하기로 했다.
1. 유전자 알고리즘은 일단 무작위로 임의의 갯수로 답을 찾는다. 그리고 이를 모집단으로 사용하여 가장 적은 비용을 갖는 몇 개의 해답을 골라내고(엘리트), 이 해답들을 약간 비틀어(변이를 일으켜) 다시 같은 작업을 반복한다. 이렇게 하면 좋은 답에서 얻어진 유전자를 바탕으로 더 좋은 답을 얻을 수 있다는 것이 유전자 알고리즘의 기본 사상이다.
내가 풀고자 하는 문제는 찾아야 할 것이, 주가 추세 직선을 구성하는 점의 갯수와 그 점의 위치이다. 여기서 어떤 것을 변이시킬지 찾아야 한다. 여기서 점 자체를 변이시키면 변이에 대한 경우의 수가 너무 많다. 해서 점의 갯수를 변이 시키기로 하고, 그에 따라 현재 물려받은 점 들에 새로운 점을 추가하거나, 기존의 점을 삭제하기로 했다.
$$
P_i = \{ (x_1, y_1), ... ,(x_n, y_n) | n \} \rightarrow P_{i+1} = \{(x_1, y_1), ... , (x_m, y_m)|m\}, m = n+1
$$
위의 경우는 $i$에서 $i+1$로 세대가 넘어가면서 점이 하나 추가된 경우이다. 단 기존 세대에서 받아온 점은 그대로 유지하고 새로운 점만 하나 더 추가를 한다. 이 때 추가 또는 삭제 대상 점의 선정은 무작위로 하도록 했다. 이렇게 하면 엘리트 집단 안의 하나의 엘리트는 각자 두 개의 자손(더하기, 빼기)을 갖게 된다.
앞서의 과정을 임의의 충분한 횟수만큼 돌리거나, 몇 세대동안 더이상 발전이 없을 경우(최선의 답이 바뀌지 않을 경우) 멈추는 방식으로 구현한다.
2. 이 작업을 하면서 비용 함수를 조금 손을 봤다. 일단 점의 갯수에 패널티를 줄 때, 스케일을 고려하여 점의 갯수에서 전체 데이터 수를 나누어 일종의 비율로 나타내도록 했다. 즉, 다음과 같은 비용 함수를
$$
C = \sum_{i=1}^{n}(\hat{y}_i - y_i)^2 + \omega m
$$
다음과 같이 고쳤다.
$$
C = \sum_{i=1}^{n}(\hat{y}_i - y_i)^2 + m / n
$$
여기서 $n$은 전체 데이터의 갯수이다.
그리고 여기다 하나 더 추가했다. 무릇 추세선이라고 하면 그럴싸하게 넓직하게 나와야 더 좋아보일 것이다. 그래서 점간 거리($x$의 거리)를 비용으로 추가하기로 했다. 그러면 아무래도 바로 옆 점을 추가하는데 부담을 느끼게 될 것이고 추세를 나타내는 점이 조금 더 넓게 퍼질 것으로 기대할 수 있다. 일단, 점 간거리를 다음과 같이 정의하자.
$$
D = \{x_i - x_{i-1}\}, i=2,...n
$$
이 값을 비용으로 사용하기 위해서는 점 간거리가 가까울수록 비용 부과를 더 해야하니 위의 벡터의 요소들을 각각 역수를 취하자.
$$
\hat{D}=\{ \frac{1}{x_i - x_{i-1}}\}
$$
비용은 $\hat{D}$의 각 요소의 제곱의 합으로 나타내면 되므로 $ \hat{D}^T\hat{D}$ 로 표현할 수 있다. 그래서 최종적으로 현재 구현한 비용 함수는 다음과 같다.
$$
C = \sum_{i=1}^{n}(\hat{y}_i - y_i)^2 + m / n + \hat{D}^T\hat{D}
$$
이런 식으로 찾아낸 주가 패턴 두가지를 아래 그림으로 첨부한다.
3. 이제 이런 방식으로 구해진 패턴 데이터를 어떻게 머신 러닝에 적용할 데이터로 만들지 고민해봐야 한다. 아마도 텐서플로를 기반으로 작업을 진행할 것 같으니, 앞으론 텐서플로를 정리해보도록 하겠다.
일단 지난번에 Random Optimization을 가지고 테스트를 해봤다. 최적화라는 것이 어느정도 무작위성을 가지고 있는 것은 맞다. 아무래도 처음 답을 찍어서 이리저리 흔들어보며 더 나은 방향으로 나아가기 때문일 것이다. 하지만 너무 대놓고 무작위로 답을 찾아들어가면 작업을 많이 돌리면 돌릴수록 결과가 나아질 가능성이 높아지긴 하나 그 보장이 없으므로 무엇인가 안정적이면서 멋도 조금 나는 것들을 찾아보기로 했다.
최적화의 기본적인 알고리즘인 Hill Climb의 경우 이웃 해답이라는 개념이 있어야 하는데, 내가 풀고자 하는 문제에서는 이웃 해답을 정의하기가 애매했다. 그래서 멋도 나고 쓸만한 것으로 유전자 알고리즘을 선택하기로 했다.
1. 유전자 알고리즘은 일단 무작위로 임의의 갯수로 답을 찾는다. 그리고 이를 모집단으로 사용하여 가장 적은 비용을 갖는 몇 개의 해답을 골라내고(엘리트), 이 해답들을 약간 비틀어(변이를 일으켜) 다시 같은 작업을 반복한다. 이렇게 하면 좋은 답에서 얻어진 유전자를 바탕으로 더 좋은 답을 얻을 수 있다는 것이 유전자 알고리즘의 기본 사상이다.
내가 풀고자 하는 문제는 찾아야 할 것이, 주가 추세 직선을 구성하는 점의 갯수와 그 점의 위치이다. 여기서 어떤 것을 변이시킬지 찾아야 한다. 여기서 점 자체를 변이시키면 변이에 대한 경우의 수가 너무 많다. 해서 점의 갯수를 변이 시키기로 하고, 그에 따라 현재 물려받은 점 들에 새로운 점을 추가하거나, 기존의 점을 삭제하기로 했다.
$$
P_i = \{ (x_1, y_1), ... ,(x_n, y_n) | n \} \rightarrow P_{i+1} = \{(x_1, y_1), ... , (x_m, y_m)|m\}, m = n+1
$$
위의 경우는 $i$에서 $i+1$로 세대가 넘어가면서 점이 하나 추가된 경우이다. 단 기존 세대에서 받아온 점은 그대로 유지하고 새로운 점만 하나 더 추가를 한다. 이 때 추가 또는 삭제 대상 점의 선정은 무작위로 하도록 했다. 이렇게 하면 엘리트 집단 안의 하나의 엘리트는 각자 두 개의 자손(더하기, 빼기)을 갖게 된다.
앞서의 과정을 임의의 충분한 횟수만큼 돌리거나, 몇 세대동안 더이상 발전이 없을 경우(최선의 답이 바뀌지 않을 경우) 멈추는 방식으로 구현한다.
2. 이 작업을 하면서 비용 함수를 조금 손을 봤다. 일단 점의 갯수에 패널티를 줄 때, 스케일을 고려하여 점의 갯수에서 전체 데이터 수를 나누어 일종의 비율로 나타내도록 했다. 즉, 다음과 같은 비용 함수를
$$
C = \sum_{i=1}^{n}(\hat{y}_i - y_i)^2 + \omega m
$$
다음과 같이 고쳤다.
$$
C = \sum_{i=1}^{n}(\hat{y}_i - y_i)^2 + m / n
$$
여기서 $n$은 전체 데이터의 갯수이다.
그리고 여기다 하나 더 추가했다. 무릇 추세선이라고 하면 그럴싸하게 넓직하게 나와야 더 좋아보일 것이다. 그래서 점간 거리($x$의 거리)를 비용으로 추가하기로 했다. 그러면 아무래도 바로 옆 점을 추가하는데 부담을 느끼게 될 것이고 추세를 나타내는 점이 조금 더 넓게 퍼질 것으로 기대할 수 있다. 일단, 점 간거리를 다음과 같이 정의하자.
$$
D = \{x_i - x_{i-1}\}, i=2,...n
$$
이 값을 비용으로 사용하기 위해서는 점 간거리가 가까울수록 비용 부과를 더 해야하니 위의 벡터의 요소들을 각각 역수를 취하자.
$$
\hat{D}=\{ \frac{1}{x_i - x_{i-1}}\}
$$
비용은 $\hat{D}$의 각 요소의 제곱의 합으로 나타내면 되므로 $ \hat{D}^T\hat{D}$ 로 표현할 수 있다. 그래서 최종적으로 현재 구현한 비용 함수는 다음과 같다.
$$
C = \sum_{i=1}^{n}(\hat{y}_i - y_i)^2 + m / n + \hat{D}^T\hat{D}
$$
이런 식으로 찾아낸 주가 패턴 두가지를 아래 그림으로 첨부한다.
3. 이제 이런 방식으로 구해진 패턴 데이터를 어떻게 머신 러닝에 적용할 데이터로 만들지 고민해봐야 한다. 아마도 텐서플로를 기반으로 작업을 진행할 것 같으니, 앞으론 텐서플로를 정리해보도록 하겠다.
조금 더 복잡한 Chain Rule
0. PDE를 써서 FDM으로 만들 때 복잡한 수식을 변환하거나, 격자 자체의 방향을 틀어버리는 목적으로 변수 치환을 많이 한다. 그 때 연산자 변환을 위해서 chain-rule을 자주 사용하는데, 2차 미분으로 넘어가면서 헷갈리는 경우가 많아 정리를 해두려 한다.
1. 복잡한 chain-rule에 대해 이해를 해보려다가 인터넷을 뒤적거리다 보니, 꽤 괜찮은 방법을 찾았다. 그 것은 바로 일종의 이항트리를 이용하는 방식이다. 다음과 같은 함수가 있다고 가정하자.
여기서 $x$와 $y$를 변수로 갖는 함수를 $f(x, y)$로 하고 $\psi$와 $\eta$를 변수로 갖는 함수를 $g(\psi, \eta)$라고 하자. 여기서 $f(.) = g(.)$이라 하면, 내가 관심있는 것은 $\partial{f} / \partial{x}$를 어떻게 $\psi$와 $\eta$에 대해 변환할 수 있을까이다.
변환을 시작하기 전에 다음과 같은 다이어그램을 그려보자.
$ g \\
/ \backslash \\
\psi \eta \\
/ \backslash / \backslash \\
x y x y $
뭔가 좀 후지긴 한데... 어쨌든, $g$는 $\psi, \eta$의 함수이고, 또 각각은 $x, y$의 함수라는 의미이다. 그래서 chain-rule을 이용하여 미분을 할 때 각 트리를 따라 내려가면 수월하게 할 수 있다. 트리의 가지를 하나 내려올 때마다 미분이 추가된다고 보면 된다. 즉, $g$에서 $\psi$로 오면 $g$를 $\psi$로, $\psi$에서 $x$로 오면 $\psi$를 $x$로 미분한다는 의미이다.
2. 1차 미분
$\partial{f}/\partial{x}$를 변환하기 위해서, 즉 $\partial{g}/\partial{x}$를 찾기 위해서는 위 트리를 따라 내려가며 $x$가 나올 수 있는 경우를 모두 찾는다. 여기서는 $g \rightarrow \psi \rightarrow x$와 $g \rightarrow \eta \rightarrow x$의 두가지가 있다. 즉, $\psi, \eta$ 각각에 대해 미분을 해줘야 한다는 의미이다. 그래서 종합하면 다음과 같다.
$$ \frac{\partial f}{\partial x} = \frac{\partial g}{\partial \psi} \frac{\partial \psi}{\partial x} + \frac{\partial g}{\partial \eta} \frac{\partial \eta}{\partial x} $$ 그리고 앞에 정의한 $\psi, \eta$를 $x$에 대해 미분해서 넣어주면 다음과 같은 결과가 나온다.
$$ \frac{\partial f}{\partial x} = \frac{\partial g}{\partial \psi} + \frac{\partial g}{\partial \eta} ... (1)$$
만약 $y$에 대해서 찾는다면 위와 같은 방식으로 트리를 타고 내려오면 쉽게 이해할 수 있다.
3. 2차 미분
이제 $\partial^2 f/\partial{x}^2$를 변환하고 싶다. 그럼 앞의 그래프에서 $g$를 (1)번 식의 각 항으로 바꾸어 각각 진행한다. 즉, 두 항에 대해 앞과 같은 그래프 태우기를 한다. 그럼 다음과 같은 순서로 진행된다.
$$ \frac{\partial^2 f}{\partial{x}^2} = \frac{\partial}{\partial x} (\frac{\partial g}{\partial \psi} +
\frac{\partial g}{\partial \eta} ) \\ = (\frac{\partial^2 g}{\partial{\psi}^2} \frac{\partial{\psi}}{\partial x}
+ \frac{\partial^2 g}{\partial{\psi}\partial{\eta}}\frac{\partial \eta}{\partial x})
+ (\frac{\partial^2 g}{\partial{\eta}^2} \frac{\partial{\eta}}{\partial x}
+ \frac{\partial^2 g}{\partial{\psi}\partial{\eta}}\frac{\partial \psi}{\partial x}) $$
즉, 트리의 각 가지를 타고 내려오며 해당 미분을 해주면 된다는 의미다.
4. 합성 미분
합성 미분도 위의 방식대로 $x$가 필요할 때는 $x$를 찾는 방향으로, $y$가 필요하면 $y$를 찾는 방향으로 움직이면 된다.
1. 복잡한 chain-rule에 대해 이해를 해보려다가 인터넷을 뒤적거리다 보니, 꽤 괜찮은 방법을 찾았다. 그 것은 바로 일종의 이항트리를 이용하는 방식이다. 다음과 같은 함수가 있다고 가정하자.
$$ \psi = x+y, \eta = x-y $$
여기서 $x$와 $y$를 변수로 갖는 함수를 $f(x, y)$로 하고 $\psi$와 $\eta$를 변수로 갖는 함수를 $g(\psi, \eta)$라고 하자. 여기서 $f(.) = g(.)$이라 하면, 내가 관심있는 것은 $\partial{f} / \partial{x}$를 어떻게 $\psi$와 $\eta$에 대해 변환할 수 있을까이다.
변환을 시작하기 전에 다음과 같은 다이어그램을 그려보자.
$ g \\
/ \backslash \\
\psi \eta \\
/ \backslash / \backslash \\
x y x y $
뭔가 좀 후지긴 한데... 어쨌든, $g$는 $\psi, \eta$의 함수이고, 또 각각은 $x, y$의 함수라는 의미이다. 그래서 chain-rule을 이용하여 미분을 할 때 각 트리를 따라 내려가면 수월하게 할 수 있다. 트리의 가지를 하나 내려올 때마다 미분이 추가된다고 보면 된다. 즉, $g$에서 $\psi$로 오면 $g$를 $\psi$로, $\psi$에서 $x$로 오면 $\psi$를 $x$로 미분한다는 의미이다.
2. 1차 미분
$\partial{f}/\partial{x}$를 변환하기 위해서, 즉 $\partial{g}/\partial{x}$를 찾기 위해서는 위 트리를 따라 내려가며 $x$가 나올 수 있는 경우를 모두 찾는다. 여기서는 $g \rightarrow \psi \rightarrow x$와 $g \rightarrow \eta \rightarrow x$의 두가지가 있다. 즉, $\psi, \eta$ 각각에 대해 미분을 해줘야 한다는 의미이다. 그래서 종합하면 다음과 같다.
$$ \frac{\partial f}{\partial x} = \frac{\partial g}{\partial \psi} \frac{\partial \psi}{\partial x} + \frac{\partial g}{\partial \eta} \frac{\partial \eta}{\partial x} $$ 그리고 앞에 정의한 $\psi, \eta$를 $x$에 대해 미분해서 넣어주면 다음과 같은 결과가 나온다.
만약 $y$에 대해서 찾는다면 위와 같은 방식으로 트리를 타고 내려오면 쉽게 이해할 수 있다.
3. 2차 미분
이제 $\partial^2 f/\partial{x}^2$를 변환하고 싶다. 그럼 앞의 그래프에서 $g$를 (1)번 식의 각 항으로 바꾸어 각각 진행한다. 즉, 두 항에 대해 앞과 같은 그래프 태우기를 한다. 그럼 다음과 같은 순서로 진행된다.
$$ \frac{\partial^2 f}{\partial{x}^2} = \frac{\partial}{\partial x} (\frac{\partial g}{\partial \psi} +
\frac{\partial g}{\partial \eta} ) \\ = (\frac{\partial^2 g}{\partial{\psi}^2} \frac{\partial{\psi}}{\partial x}
+ \frac{\partial^2 g}{\partial{\psi}\partial{\eta}}\frac{\partial \eta}{\partial x})
+ (\frac{\partial^2 g}{\partial{\eta}^2} \frac{\partial{\eta}}{\partial x}
+ \frac{\partial^2 g}{\partial{\psi}\partial{\eta}}\frac{\partial \psi}{\partial x}) $$
즉, 트리의 각 가지를 타고 내려오며 해당 미분을 해주면 된다는 의미다.
4. 합성 미분
합성 미분도 위의 방식대로 $x$가 필요할 때는 $x$를 찾는 방향으로, $y$가 필요하면 $y$를 찾는 방향으로 움직이면 된다.
Machine Learning을 이용한 주가패턴 분석(1) - Cost Function, Random Optimization
0. 시작
최근 AI가 화두인지라 귀가 얇은 나도 역시 관심을 갖게 되었다. 그리고 업 자체가 금융업이다보니 시장을 AI를 이용하여 분석한다면 무엇인가 괜찮은 프로젝트가 나올 것 같다는 생각이 들었다. 하여, 주가패턴을 분석하는 프로젝트를 시작하고자 한다. 앞으로 올릴 포스트들은 그 프로젝트를 진행하면서 진행 상황을 기록하기 위한 목적이다.
1. 방법론 선택
일단 주가 차트를 분석하기 위해서는 일정 기간의 주가 차트를 일정한 패턴으로 만들어내야 한다. 결국 추세를 어떻게 표현할지가 관건이다. 추세를 나타내는 방법은 MA(Moving Average)를 그린다든가 어떤 Regression 기법을 이용하여 그리는 방법을 사용할 수 있을 것이다. 하지만 이 방법들은 추세 표현력은 좋으나 Machine Learning을 사용하기 위한 데이터로 전환할 수 있는 방법이 쉽게 떠오르지 않았다. 그래서 더 단순하고 직관적인 방법을 찾으려 했다.
나의 멘토이신 C박사님의 아이디어는 주가 차트를 임의의 직선의 조합으로 나타내 보자는 것이었고, 이 방식이라면 패턴 분석용 데이터를 만드는데 더 수월할 것이라는 판단이 들었다. 직선의 경우 기울기, 시작점, 끝점으로 단순히 표현할 수 있기 때문이다. 그래서 최적화 기법을 이용하여 직선 및 점의 갯수를 찾아내고 그 데이터를 이용하여 패턴 분석을 하기로 했다.
2. 프로그래밍 언어
일단 최적화를 구현하기 위한 언어는 R로 선택하였다. 처음에 python과 R을 모두 고민했으나, 내 손에 편하고 데이터 분석에 강점이 있는 R을 사용하기로 했다.
3. 데이터
주가 데이터는 팀 내의 데이터베이스 또는 블룸버그 터미널을 이용하여 S&P500 주가를 다운받아서 사용하였다. 단, 주가 자체의 값을 그대로 데이터로 이용할 경우 Cost Function을 구현하는데 있어 어떤 가중치를 정하는데 지수마다 달라질 수 있으므로, 주가를 정규화(normalization)을 한다. 여기서는 나에게 매우 익숙한 로그 수익률을 사용하였다.
여기서 $y_i$는 정규화한 수익률이고 $S_i$는 포인트의 주가, $S_0$는 시작 지점의 주가이다. 그리고 x축의 경우 휴일 등의 변수가 있으므로 날짜로 하기보단 1부터 n까지의 정수를 사용하기로 했다.
4. Cost Function(비용 함수)
최적화를 하기 위해서는 비용 함수가 중요하다. 이는 내가 생각한 답이 어느정도의 오류를 가지고 있는지 표현하기 위한 함수이다. 최적화는 이 오류(비용) 값을 가장 적게 할 수 있는 답을 찾는 것이다. 비용 함수에서 비용은 '직선 추정치($\hat{y}$)과 실제 주가수익률($y$)의 차이'가 하나 있고, 추정을 위해 사용하는 점의 수가 너무 많을 경우 overfitting의 문제가 있으므로 점의 갯수도 비용으로 들어가야 한다.
주가 추정에 의한 차이는 잘 알려진 Least square로 하고 점의 갯수에 의한 패널티는 간단하게 일정 가중치를 점의 갯수에 곱하여 더하기로 했다.
여기서 $n$은 전체 점의 갯수이고, $m$은 직선을 구성하기 위한 점의 수이다. 그리고 $\omega$는 패널티를 주기 위한 가중치인데, 앞으로 이 값을 어떻게 조절하느냐가 꽤 중요할 것이다. 이제 이 비용 함수를 이용하여 최적화 기법을 구현해보도록 하자
5. 가장 단순한 Random Search
Random Search는 말 그대로 무작위로 추정용 점의 갯수와 위치를 찾는 방법이다. 테스트를 할 때 1만번을 돌도록 구현했고, 이 방법은 추후 구현할 최적화 기법과의 비교 용도로 사용할 것이다. 아래 간단한 결과 그래프를 첨부한다. 푸른색이 실제 주가 수익률이고 붉은색이 추정한 수익률이다.
최근 AI가 화두인지라 귀가 얇은 나도 역시 관심을 갖게 되었다. 그리고 업 자체가 금융업이다보니 시장을 AI를 이용하여 분석한다면 무엇인가 괜찮은 프로젝트가 나올 것 같다는 생각이 들었다. 하여, 주가패턴을 분석하는 프로젝트를 시작하고자 한다. 앞으로 올릴 포스트들은 그 프로젝트를 진행하면서 진행 상황을 기록하기 위한 목적이다.
1. 방법론 선택
일단 주가 차트를 분석하기 위해서는 일정 기간의 주가 차트를 일정한 패턴으로 만들어내야 한다. 결국 추세를 어떻게 표현할지가 관건이다. 추세를 나타내는 방법은 MA(Moving Average)를 그린다든가 어떤 Regression 기법을 이용하여 그리는 방법을 사용할 수 있을 것이다. 하지만 이 방법들은 추세 표현력은 좋으나 Machine Learning을 사용하기 위한 데이터로 전환할 수 있는 방법이 쉽게 떠오르지 않았다. 그래서 더 단순하고 직관적인 방법을 찾으려 했다.
나의 멘토이신 C박사님의 아이디어는 주가 차트를 임의의 직선의 조합으로 나타내 보자는 것이었고, 이 방식이라면 패턴 분석용 데이터를 만드는데 더 수월할 것이라는 판단이 들었다. 직선의 경우 기울기, 시작점, 끝점으로 단순히 표현할 수 있기 때문이다. 그래서 최적화 기법을 이용하여 직선 및 점의 갯수를 찾아내고 그 데이터를 이용하여 패턴 분석을 하기로 했다.
2. 프로그래밍 언어
일단 최적화를 구현하기 위한 언어는 R로 선택하였다. 처음에 python과 R을 모두 고민했으나, 내 손에 편하고 데이터 분석에 강점이 있는 R을 사용하기로 했다.
3. 데이터
주가 데이터는 팀 내의 데이터베이스 또는 블룸버그 터미널을 이용하여 S&P500 주가를 다운받아서 사용하였다. 단, 주가 자체의 값을 그대로 데이터로 이용할 경우 Cost Function을 구현하는데 있어 어떤 가중치를 정하는데 지수마다 달라질 수 있으므로, 주가를 정규화(normalization)을 한다. 여기서는 나에게 매우 익숙한 로그 수익률을 사용하였다.
$ y_i = \ln(\frac{S_i}{S_0}), i=1, ..., n $
4. Cost Function(비용 함수)
최적화를 하기 위해서는 비용 함수가 중요하다. 이는 내가 생각한 답이 어느정도의 오류를 가지고 있는지 표현하기 위한 함수이다. 최적화는 이 오류(비용) 값을 가장 적게 할 수 있는 답을 찾는 것이다. 비용 함수에서 비용은 '직선 추정치($\hat{y}$)과 실제 주가수익률($y$)의 차이'가 하나 있고, 추정을 위해 사용하는 점의 수가 너무 많을 경우 overfitting의 문제가 있으므로 점의 갯수도 비용으로 들어가야 한다.
주가 추정에 의한 차이는 잘 알려진 Least square로 하고 점의 갯수에 의한 패널티는 간단하게 일정 가중치를 점의 갯수에 곱하여 더하기로 했다.
$ C = \sum_{i=1}^{n}(\hat{y}_i - y_i)^2 + \omega m $
여기서 $n$은 전체 점의 갯수이고, $m$은 직선을 구성하기 위한 점의 수이다. 그리고 $\omega$는 패널티를 주기 위한 가중치인데, 앞으로 이 값을 어떻게 조절하느냐가 꽤 중요할 것이다. 이제 이 비용 함수를 이용하여 최적화 기법을 구현해보도록 하자
5. 가장 단순한 Random Search
Random Search는 말 그대로 무작위로 추정용 점의 갯수와 위치를 찾는 방법이다. 테스트를 할 때 1만번을 돌도록 구현했고, 이 방법은 추후 구현할 최적화 기법과의 비교 용도로 사용할 것이다. 아래 간단한 결과 그래프를 첨부한다. 푸른색이 실제 주가 수익률이고 붉은색이 추정한 수익률이다.
확실히 뭔가 어중간한 느낌은 있으나 나름 잘 찾아낸 것 같다. 앞으로 다양한 최적화 알고리즘을 구현하면서 그 결과를 살펴볼 것이다.
A Brief History of Time - Stephen Hawking
0. 선물받은 킨들의 첫 도서이다. 아무래도 공대생이지만 물리학에 약해 읽는데 걱정이 많았으나, 그래도 꽤 부드럽게 읽을 수 있었다. 물론 책 중반부터 아무리 쉽게 얘기하고 싶어도 애초에 어려운 내용들을 풀어나가다보니 한 번 읽어서 이해 안되는 부분이 꽤 많았다. (그렇다고 다시 읽거나 하진 않았다. -_-)
1. 고전의 시대부터 사람들은 주변에 관심을 갖고, 자신만의 생각을 발전시킨다. 지구와 우주의 구성을 땅, 물, 불 등이라고 생각했던 고대 철학자, 우주의 중심을 지구라 생각했던 종교인들도 있었다. 그리고 시간이 지나며 많은 사람들이 관찰하고 실험하고 이론을 만들면서 과학이 발전한다.
인간의 우주를 이해하고자하는 끝없는 노력은 우주를 설명하고자 하는 하나의 통합하는 이론을 만드는 것을 지향점으로 삼는다.
2. 뉴턴부터 시작되는 역학은 아이인슈타인의 상대성 이론을 거쳐 불확실성을 고려하는 양자역학으로 흐르고, 쿼크와 전자의 저에너지부터 빅뱅과 우주 생성을 생각하는 고에너지까지 사람의 과학적 호기심과 탐구는 우주의 진리를 찾기위해 동분서주한다. 하지만 그 어느 것도 완벽하게 우주를 하나의 모습으로 설명할 수 없다는 것은, 아직 인간이 관찰하고 실험할 수 있는 영역은 우주의 크기에 비해 매우 적다는 것으로 이해되고, 그와 더불어 그렇게 상상력을 발휘하여 이만큼 발전시킨 것도 정말 놀랍다고 할 수 있다.
3. 이 책은 우주와 시간을 이해하기위한 인간의 노력을 한권에 담았다. 스티븐 호킹 박사가 워낙 물리학계의 거두이다 보니 어려운 이론도 쉽게 말로 풀어쓰는 저력이 있다. 물론 모두 다 쉬운 것은 아니고 이해를 다 할 수도 없지만, 사람들의 우주와 시간을 이해하기 위한 노력을 이렇게 한 눈으로 볼 수 있다는 것은 정말 행운이리라.
피드 구독하기:
덧글 (Atom)
인생논어 - 1
0. 조형권님이 쓴 <<인생논어>> 를 읽고 필사한다는 생각으로 구문들을 옮겨 적으려 한다. 1. 나만의 속도를 유지하라. 子曰, 射不主皮 爲力不同科 古之道也 (자왈, 사부주피 위력부동과 고지도야) 해석: 활을 쏠 때 ...