1. 시계열 분석
시계열이란 시간 순서대로 관찰한 어떠한 값의 모음을 이야기한다. 어떤 주가 지수의 종가를 날짜별로 나열한 값이나, 시점에 따른 직장인 평균 월급을 모아놓은 값 등이 예제가 될 수 있다.
시계열 분석은 이 데이터를 가지고 어떤 일이 일었났는가를 추론한다. 그리고 그 추론을 바탕으로 미래값을 예측하는 방법이다.
일반적으로 시계열은 다음과 같은 특성을 지닌다.
- Trend - trend는 시계열이 지니고 있는 방향성을 의미한다. 방향성은 deterministic할 수도 있고, stochastic할 수도 있다.
- Seasonal Variation - 주기에 따른 시계열의 변화를 의미한다. 예를들어 천연가스의 사용량은 계절에 따라 주기성을 보인다.
- Serial Dependence - 시계열의 시간에 따른 관찰 결과가 어떤 상관관계를 갖을 수 있다. 금융 시계열 분석에서 매우 중요하게 생각하는 serial correlation으로 나타낸다.
2. 시계열의 Stationarity
Stationarity는 시계열 분석에 있어 중요한 부분을 차지한다. 많은 금융 데이터 시계열분석이 stationarity를 염두해두고 수행된다. 시계열의 stationarity를 이야기하기 위해서 시계열의 expectation(기대값)과 variance(분산)을 이야기해야 한다.
우선 시계열 $x_t$의 기대값(평균)은 $t$의 함수인 $\mu(t)$로 나타내며, $\mathbf{E}(x_t)=\mu(t)$로 표현한다. 평균, 분산 등을 구하기 위한 시계열이 여러개일 수 있지만, 일반적으로 하나의 시계열을 가지고 작업하는 경우가 많다. 시계열이 하나라면, 평균을 구하기위해 다음의 두가지 방법을 고려할 수 있다.
- 관찰한 데이터를 바탕으로 각 점에서 단순히 평균을 구하는 방법
- 시계열 데이터에서 trend, seasonality 효과를 제거하여 residual series를 만든다. 이 경우 만들어진 residual series가 stationarity in the mean(안정적 평균) 상태임을 가정할 수 있다. 그래서 상수의 $\bar{x} = \sum^{n}_{t=1} x_t/n$로 평균을 추정한다.
앞서 'stationarity in the mean'은 $\mu(t) = \mu$를 의미한다. 즉, 시계열이 시간에 관계없이 항상 동일한 평균을 갖는다는 의미이다. 시계열이 이 상태라면 분산을 다음과 같이 구한다.
$$
\sigma^2 = \mathbf{E}[(x_t - \mu)^{2}]
$$
\sigma^2 = \mathbf{E}[(x_t - \mu)^{2}]
$$
이 때 역시 시계열이 하나밖에 없을 경우, 분산이 시간에 관계없이 일정하다고 가정하고 sample variance를 구하는 방법이 있다.
$$
\mathbf{Var}(x) = \frac{\sum(x_t - \bar{x})^2}{n-1}
$$
이 경우 이 시계열을 stationarity in the variance(안정적 분산) 상태라고 부른다.
Serial correlation을 위해 우선 lag라는 개념을 보자. Lag는 하나의 전체 시계열이 있을 때 시간 차를 두고 추출한 하위 시계열이다. 예를 들어 시계열 $\vec{x}_{t} = \{x_t, x_{t-1}, x_{t-2} ... x_{0}\}$가 있다고 하자. 여기서 lag이 1일 때 시계열은 $\vec{x}_{t+1} = \{x_{t+1}, x_{t}, x_{t-1} ... x_{1}\}$이 된다.
이렇게 lag를 건너 뛴 시계열도 하나의 또 다른 시계열로 볼 수 있다. 그래서 두 시계열간의 상관관계가 존재한다. 이 때 이 상관관계가 $t$의 함수가 아니라 lag를 의미하는 $k$의 함수로 나타낼 수 있다면, 이런 경우를 'Second order stationary'상태라 한다.
시계열이 second order stationary 상태라면, 두 시계열간 공분산(autocovariance)을 다음과 같이 구할 수 있다.
$$
C_k = \mathbf{E}[(x_t - \mu)(x_{x+k} - \mu)]
$$
잘 보면 이 second order stationary가 앞서 이야기한 mean, variance의 stationary를 포함하는 것으로 볼 수 있다.
이렇게 구해진 autocovariance를 이용하여 serial correlation(autucorrelation)을 다음과 같이 구할 수 있다.
$$
\rho_k = \frac{C_k}{\sigma^2}
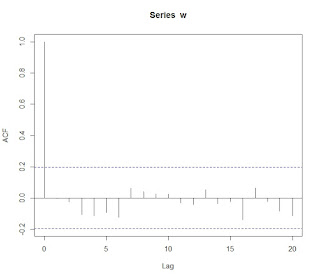
$$
다음의 차트는 100개의 난수로 이루어진 시계열의 correlogram(lag별 autocorrelation 차트)이다.
난수의 시계열이므로 lag가 0인경우만 serial correlation이 1이고 나머지는 거의 0에 수렴한다.
다음은 1부터 100까지의 수열에 대한 차트이다.
Lag값이 커질수록 값이 줄어들지만, 전반적으로 높은 수준의 상관관계를 보여준다.
마지막으로 반족되는 수열의 차트이다.
차트에서 보듯이 반복 주기마다 상관계수가 높아지는 것을 확인할 수있다.
$$
\mathbf{Var}(x) = \frac{\sum(x_t - \bar{x})^2}{n-1}
$$
이 경우 이 시계열을 stationarity in the variance(안정적 분산) 상태라고 부른다.
3. Serial Correlation
Serial correlation을 위해 우선 lag라는 개념을 보자. Lag는 하나의 전체 시계열이 있을 때 시간 차를 두고 추출한 하위 시계열이다. 예를 들어 시계열 $\vec{x}_{t} = \{x_t, x_{t-1}, x_{t-2} ... x_{0}\}$가 있다고 하자. 여기서 lag이 1일 때 시계열은 $\vec{x}_{t+1} = \{x_{t+1}, x_{t}, x_{t-1} ... x_{1}\}$이 된다.
이렇게 lag를 건너 뛴 시계열도 하나의 또 다른 시계열로 볼 수 있다. 그래서 두 시계열간의 상관관계가 존재한다. 이 때 이 상관관계가 $t$의 함수가 아니라 lag를 의미하는 $k$의 함수로 나타낼 수 있다면, 이런 경우를 'Second order stationary'상태라 한다.
시계열이 second order stationary 상태라면, 두 시계열간 공분산(autocovariance)을 다음과 같이 구할 수 있다.
$$
C_k = \mathbf{E}[(x_t - \mu)(x_{x+k} - \mu)]
$$
잘 보면 이 second order stationary가 앞서 이야기한 mean, variance의 stationary를 포함하는 것으로 볼 수 있다.
이렇게 구해진 autocovariance를 이용하여 serial correlation(autucorrelation)을 다음과 같이 구할 수 있다.
$$
\rho_k = \frac{C_k}{\sigma^2}
$$
4. 예제
다음의 차트는 100개의 난수로 이루어진 시계열의 correlogram(lag별 autocorrelation 차트)이다.
다음은 1부터 100까지의 수열에 대한 차트이다.
마지막으로 반족되는 수열의 차트이다.
댓글 없음:
댓글 쓰기