1. 시계열 모형을 다루는 과정
시계열 모형은 시계열에 있는 serial correlation을 설명하기위한 수학모형이다. 여기서 설명한다는 의미는 다음과 같다. 일단 지정한 모형을 시계열에 맞추면(fitting), correlogram에서 보이는 해당 시계열의 serial correlation을 대부분 설명할 수 있어야 한다.
모형을 선택하고 맞춰가는 과정은 다음과 같이 요약할 수 있다.
- 특정 시계열과 그 움직임에 대한 가설의 윤곽을 잡는다
- R 등의 도구를 이용하여 해당 시계열의 correlogram을 그려본다.
- 오류항(residuals)의 serial correlation을 줄이는 모형을 찾아 맞춘다
- 반복적으로 serial correlation을 없애는 방향으로 맞춰보고 통계 테스트를 수행한다
- 모형과 모형의 'second-order properties'를 이용하여 미래값을 예측한다.
- 예측의 정확도가 최적일 때까지 반복한다.
여기서 'second-order properties'는 앞 포스트에서 얘기한 평균, 분산, serial correlation의 특성을 지칭한다.
모형을 설명하기에 앞서 두 가지 연산자를 소개하고 넘어가려 한다.
- Backward shift operator (lag operator) - $\mathbf{B}$로 표현하며 $\mathbf{B}x_t = x_{t-1}$이다. 반복 적용하면 $\mathbf{B}^n x_t = x_{t-n}$이 된다.
- Difference operator - 표현은 $\nabla$로 한다. 라플라스 연산자(Laplace operator)와 같은 모양인데, 이 책에서는 difference로 사용한다. $\nabla x_t = x_t - x_{t-1}$ 또는 $\nabla x_t = (1-\mathbf{B})x_t$이다.
2. White Noise
White noise 모형은 방향성이 없는 모형이며, 주로 오류항의 시계열을 나타내기위해 사용한다. $y_t$가 관찰한 값의 시계열이고, $\hat{y}_t$가 예측치라면, 오류항의 시계열 $x_t$는 $y_t - \hat{y}_t$이다.
만약 적당한 시계열 모형을 선택했다면, 모형으로 측정한 값과 실측값의 차이(오류 시계열)의 serial correlation은 거의 없게 된다. 즉, 오류 자체가 white noise로서 서로 독립적인 값이 되므로 새로운 모형을 적용할 여지가 없어진다.
White noise의 second-order properties는 다음과 같다.
$$ \begin{eqnarray}
& \mu_{\omega} = \mathbf{E}(\omega_t) = 0 \\
& \rho_k = \mathbf{Cor}(\omega_t, \omega_{t+k}) =
\left\{ \begin{array} \\
1, k = 0 \\
0, k \not= 0
\end{array} \right. \end{eqnarray}
$$
그리고 correlogram은 다음과 같이 나타난다.
Random walk 시계열 모형은 직전 시계열 값에 오류항을 더한 식으로 표현한다.
$$
x_t = \mathbf{B}x_t + \omega_t = x_{t-1} + \omega_t
$$
위의 식을 반복하여 적용하면 다음과 같은 식을 얻을 수 있다.
$$
x_t = (1 + \mathbf{B} + \mathbf{B}^2 + \dots )\omega_t \Longrightarrow x_t = \sum_{i=0}^n \omega_{t-i}
$$
즉, random walk는 서로 독립인 오류항의 합으로 나타난다.
오류항의 분산이 $\sigma^2$라고 하면, random walk의 second-order properties는 다음과 같다.
$$
\begin{eqnarray}
&\mu_x = 0 \\
&\gamma_k(t) = \mathbf{Cov}(x_t, x_{t+k}) = t\sigma^2 \\
&\rho_k(t) = \frac{\mathbf{Cov}(x_t, x_{t+k})}{\sqrt{\mathbf{Var}(x_t)\mathbf{Var}(x_{t+k})}} = \frac{t\sigma^2}{\sqrt{t\sigma^2(t+k)\sigma^2}} = \frac{1}{\sqrt{1+k/t}} \end{eqnarray}
$$
위의 식에서 볼 수 있듯이, random walk의 공분산이 $k$가 아닌 $t$의 함수이다. 그러므로 random walk는 non-stationary 시계열 모형이다. 이 모형의 correlogram은 다음과 같다.
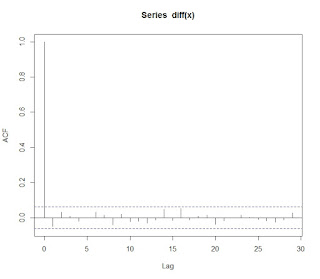
$\nabla x_t = x_t - x_{t-1}$의 correlogram을 그려본다. 이 작업은 random walk로 생성한 데이터를 random walk 모형으로 추정했다고 가정했을 때, 오류항의 serial correlation을 볼 수 있는 작업이다.
& \mu_{\omega} = \mathbf{E}(\omega_t) = 0 \\
& \rho_k = \mathbf{Cor}(\omega_t, \omega_{t+k}) =
\left\{ \begin{array} \\
1, k = 0 \\
0, k \not= 0
\end{array} \right. \end{eqnarray}
$$
그리고 correlogram은 다음과 같이 나타난다.
3. Random Walk
Random walk 시계열 모형은 직전 시계열 값에 오류항을 더한 식으로 표현한다.
$$
x_t = \mathbf{B}x_t + \omega_t = x_{t-1} + \omega_t
$$
위의 식을 반복하여 적용하면 다음과 같은 식을 얻을 수 있다.
$$
x_t = (1 + \mathbf{B} + \mathbf{B}^2 + \dots )\omega_t \Longrightarrow x_t = \sum_{i=0}^n \omega_{t-i}
$$
즉, random walk는 서로 독립인 오류항의 합으로 나타난다.
오류항의 분산이 $\sigma^2$라고 하면, random walk의 second-order properties는 다음과 같다.
$$
\begin{eqnarray}
&\mu_x = 0 \\
&\gamma_k(t) = \mathbf{Cov}(x_t, x_{t+k}) = t\sigma^2 \\
&\rho_k(t) = \frac{\mathbf{Cov}(x_t, x_{t+k})}{\sqrt{\mathbf{Var}(x_t)\mathbf{Var}(x_{t+k})}} = \frac{t\sigma^2}{\sqrt{t\sigma^2(t+k)\sigma^2}} = \frac{1}{\sqrt{1+k/t}} \end{eqnarray}
$$
위의 식에서 볼 수 있듯이, random walk의 공분산이 $k$가 아닌 $t$의 함수이다. 그러므로 random walk는 non-stationary 시계열 모형이다. 이 모형의 correlogram은 다음과 같다.
댓글 없음:
댓글 쓰기