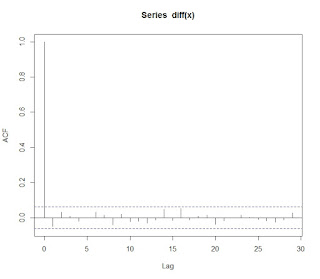
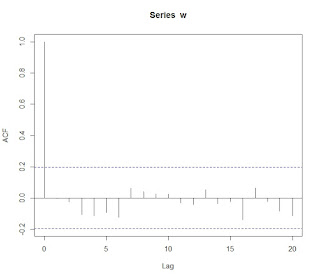
1. ARIMA(Autoregressive Integrated Moving average)
ARMA 모형의 경우 불안정(non-stationary) 시계열을 모델링하는데 적합하지 않다. 하지만 불안정 시계열의 차분을 새로운 시계열로 만들면 안정적(stationary) 시계열이 될 수 있다. 이 점이 ARIMA 모형을 사용하게하는 중요한 이유이다.
ARIMA 모형은 ARIMA(p, d, q)로 표현한다. 여기서 p와 q는 앞선 포스트에서 소개한 AR과 MA의 차수이고, d는 몇 번의 차분을 수행하는가의 의미이다. (차분이 왜 integrated라는 이름을 달고있는가는 이해하지 못했다.)
ARIMA(p, d, q)는 d번의 차분을 시계열에 수행했을 때, 그 시계열이 ARMA(p, q) 모형을 따른다는 의미이다. 이를 식으로 정의하면 다음과 같다.
$$
\theta_p(\mathbf{B})(1-\mathbf{B})^d x_t = \phi_q(\mathbf{B})\omega_t
$$
이식을 ARMA(p, q)를 나타내는 $\theta_p(\mathbf{B})x_t = \phi_q(\mathbf{B})\omega_t$와 비교하면 그 차이를 명확히 알 수 있다.
다음의 코드는 Amazon의 시계열을 받아와 ARIMA모형으로 피팅하는 R 코드이다.
require(quantmod)
getSymbols("AMZN", src="google")
# close price
amzn = diff(log(Cl(AMZN)))
plot(amzn)
# remove na
ft <- as.numeric(amzn)
ft <- ft[!is.na(ft)]
# fitting ARIMA
ftfinal.aic <- Inf
ftfinal.order <- c(0, 0, 0)
for(p in 1:4)
{
for(d in 0:1)
{
for(q in 1:4)
{
ftcurrent.aic <- AIC(arima(ft, order=c(p, d, q)))
if(ftcurrent.aic < ftfinal.aic)
{
ftfinal.aic <- ftcurrent.aic
ftfinal.order <- c(p, d, q)
ftfinal.arima <- arima(ft, order=ftfinal.order)
}
}
}
}
ftfinal.order
이 코드에서 AIC 함수를 이용하여 ARIMA(p, d, q)의 각 차수를 결정하는 것을 볼 수 있다.
2. ARCH(Autoregressive Conditional Heteroskedastic)과 GARCH 모형
앞서 ARMA 계열의 모형은 어찌했건 시계열의 안정적 상태를 가정한다. 즉, 분산이 시점에 상관없이 같은 값을 갖는다고 가정한다. 하지만 이와 다르게 분산이 시점에 따라 달라지는 시계열을 자주 볼 수 있으며, 이를 시계열이 이분산(heteroskedastic) 특성을 갖는다고 한다. 이와 더불어 이분산 특성이 연속적으로 연관되어 나타난다면, 특정 조건하에서 이분산이 나타나는 것이므로 이를 조건부 이분산(conditional heteroskedastic) 특성이라 한다.
이런 특성을 갖는 시계열을 분석하기 위해 변동성 자체를 모형으로 만드는 ARCH나 GARCH 모형을 사용할 수 있다. 차수가 1인 ARCH(1) 모형은 시계열 $\{ \epsilon_t \}$에 대해 다음과 같이 정의한다.
$$
\epsilon_t = \sigma_t \omega_t \\
\sigma_t^2 = \alpha_0 + \alpha_1 \epsilon_{t-1}^2
$$
위의 식을 $\epsilon_t$에 대해 풀면 다음과 같다.
$$
\epsilon_t = \omega_t \sqrt{\alpha_0 + \alpha_1 \epsilon_{t-1}^2}
$$
위의 식을 p 차수로 확장한 ARCH(p)의 식은 다음과 같다.
$$
\epsilon_t = \omega_t \sqrt{\alpha_0 + \sum_{i=1}^p \alpha_i \epsilon_{t-i}^2}
$$
여기서 $\alpha$는 모형 인수이다.
GARCH(Generalized Autoregressive Conditional Heteroskedastic) 모형은 ARCH(p)를 확장한 모형으로서, GARCH(p, q)로 표현한다. 표현식은 다음과 같다.
$$
\epsilon_t = \sigma_t \omega_t \\
\sigma^2_t = \alpha_0 + \sum_{i=1}^p \alpha_i \epsilon_{t-i}^2 + \sum_{j=1}^q \beta_j \epsilon_{t-j}^2
$$
여기서 $\alpha$와 $\beta$는 모형의 인수이다. GARCH는 ARCH에 이동 평균(moving average) 항을 추가한 모형으로 이해할 수 있다.